petyr
2018-10-30 06:41:46 | dp=v*dm=v*rho*dVolume=v*rho*A*dx=v*rho*A*v*dt\r\n\r\ntherefore dp/dt=F=rho*(v^2)*A.\r\nshowbox |  |
Baharmajorana
2014-09-19 11:25:44 | I have a sulotion with Bernoulli's equation. I assum that the initial and the final situation that P1+1/2.ru.v1^2=P2+ 1/2.ru.v2^2 , then we have that the initial speed is Zeroo then we have: deltaP = 1/2 ru v^2 and F= PA , so we have F= 1/2 ru v^2 A. I think this is partially true? Hmm? |  |
beforebeing
2013-09-11 00:14:50 | Even easier, no calculus:
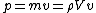
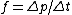
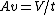 (from continuity equation) (from continuity equation)
The change in momentum is 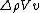 since there is no horizontal component left after the stream hits the wall. since there is no horizontal component left after the stream hits the wall.
So:
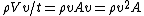 |  |
ticklecricket
2010-11-07 12:37:47 | Quick dimensional checks.
Should have a mass term, which is 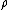 * A, so D and E are out. * A, so D and E are out.
C has a height dependence, and that doesn't make *any* sense for this problem.
Which leaves A and B, one has units of momentum and one has units of force (v vs. v^2) |  |
vtakhist
2009-10-21 06:29:59 | You can think about it as force of Drag which is proportional to the quantities in the right answer choice (A). |  |
ramparts
2009-10-08 11:09:01 | I always try to take limits first, then use dimensional analysis - looking at the units is great, but it can be time-consuming (you'd have to calculate two or three separate combinations of units here) and it's really easy to make a mistake, especially for folks like me who are really prone to making stupid mistakes. Limits are much easier.
So the force most certainly will not blow up as 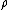 goes to 0. Much easier way of eliminating D and E than units. As Andresito said, choice C has the right units but don't bother checking, there's no h given in this problem. Finally, check the units to distinguish between A and B. You've saved two possibly mistaken units calculations :) goes to 0. Much easier way of eliminating D and E than units. As Andresito said, choice C has the right units but don't bother checking, there's no h given in this problem. Finally, check the units to distinguish between A and B. You've saved two possibly mistaken units calculations :)
BerkeleyEric
2010-07-18 19:18:38 |
I think in this case you can just check the limits of (A). Once you see that they are right, (B) can't work because there needs to be another v, (D) and (E) can't work because the rho would need to be in the numerator.
And (C) is just odd since there is no h in the problem.
|
|  |
anmuhich
2009-03-15 12:33:54 | Dimensional analysis definitely doesn't hurt in this case. Thinking about this in terms of Newtons third law with equal and opposite forces, you know that you have an amount of mass per unit time striking a wall. It's easy to see that A*v is a volume per time element. So if you multiply this times a density you get a mass per unit time. So you know that rho*v*A has to be in the answer. This is a mass per time thing. Then by looking at dimensions you know that you need another meters per time to make this mass*meters per time squared (aka Newtons). Answer A is the only answer left that makes sense because C talks about h and g which intuitively shouldn't matter at all. |  |
linford86
2009-01-07 20:39:02 | Use Bernoulli's law to get an approximation. Unfortunately, if you do this, you'll notice that you're off by a factor of a half. But none of the other choices depend quadratically on v (this comes from the kinetic energy term in Bernoulli's law; the kinetic energy is proportional to the square of the velocity.) Multiply the pressure by A to get the force from the pressure. Also, note that the fluid velocity must be zero at the wall since this is a stagnation point. |  |
michealmas
2006-12-30 13:00:19 | nice technique senvas |  |
Healeyx76
2006-11-02 19:50:13 | scottopoly, i serioulsy hope thats not true :) |  |
scottopoly
2006-10-29 23:03:11 | I heard they no longer have questions with answers that can be reduced by dimensional analysis. Am I right?
kevglynn
2006-11-03 09:05:25 |
Could you maybe tell us where you heard that? Because, well, "...frankly, it sounds made up." -Cosmo Kramer
|
jesford
2008-04-05 10:17:41 |
I have also heard something like this. Not that there are no more problems that can be solved by dimensional analysis, but that ETS has tried to cut down on the number of problems that can be solved this way.
|
|  |
senvas
2006-09-12 12:20:32 | alternatively:
dp=v*dm=v*rho*dVolume=v*rho*A*dx=v*rho*A*v*dt
therefore dp/dt=F=rho*(v^2)*A
as in choice A
Anastomosis
2008-04-10 20:05:21 |
Me love LaTeX.
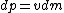
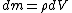
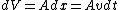
so, dividing both sides by dt:
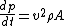
because 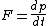
|
walczyk
2011-04-07 11:40:55 |
this is how i did it originally, then when i looked at it again i couldn't figure it out without dimensional reasoning :x. props to you good sir
|
jdbro
2014-10-24 22:32:07 |
nice
|
jdbro
2014-10-24 22:32:28 |
nice
|
|  |
Andresito
2006-03-12 16:27:15 | Actually choice (C) has the correct dimension but "h" is a variable which is irrelevant. We are assuming uniform flux of water.
thanks Yosun |  |
