GREPhysics.NET: GR0177 #56

GR0177 #56

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Mechanics $\Rightarrow$ }Fluid Statics

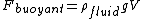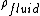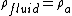The physical equation required is the buoyancy equation or Archimedes' Principal. The buoyant force is given by, $F_{buoyant} = \rho_{fluid} g V$ . $\rho_{fluid}$ refers to the density of the fluid that buoy's the object. In this case, $\rho_{fluid}=\rho_a$ is just the density of air (not Helium).

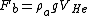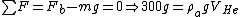The buoyant force for this problem is $F_b = \rho_a g V_{He}$ . This force must balance the load carried by the balloon. One now has (approximately, to simplify the calculations, since one is neglecting the weight of Helium) a simple sum of the forces problem, $\sum F = F_b - mg = 0 \Rightarrow 300g = \rho_a g V_{He}$ .

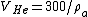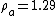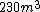Now, solving for the volume of Helium required, one has $V_{He} = 300/\rho_a$ . Since $\rho_a = 1.29$ , this is about $230 m^3$ . However, since the balloon has to lift the weight of the Helium as well, the actual volume should be slightly larger. The closest choice is (D).

Alternate Solutions

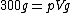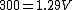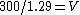tim123456789 2019-09-29 04:06:36	Archimedes Principle: The buoyant force is equal to the weight of the displaced fluid.\r\n\r\nAir is being displaced by the balloon. So:\r\n\r\n $300g = pVg$ \r\n\r\n $300 = 1.29V$ \r\n\r\n $300/1.29 = V$ \r\n\r\n1.29 is slightly larger than one, so the quotient should be slightly smaller than 300, which is (D) Reply to this comment
greenfruit 2008-11-05 08:41:46	It's really simple, conceptually. For the balloon to float: The mass of the block + the mass of the He in the balloon < the mass of the air displaced by the balloon 300kg + (x * .18 kg/m^3) <= x * 1.29 kg/m^3 with x being the volume of the balloon. Solve for x, x=270 m^3. Reply to this comment

Comments

tim123456789
2019-09-29 04:06:36

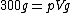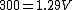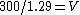Archimedes Principle: The buoyant force is equal to the weight of the displaced fluid.\r\n\r\nAir is being displaced by the balloon. So:\r\n\r\n $300g = pVg$ \r\n\r\n $300 = 1.29V$ \r\n\r\n $300/1.29 = V$ \r\n\r\n1.29 is slightly larger than one, so the quotient should be slightly smaller than 300, which is (D)

Reply to this comment

NSF Fellow
2013-10-07 11:12:44

Why don't you just do
300 / (1.29-0.18)=270

Reply to this comment

Dodobird
2010-11-01 08:14:52

The easiest way to solve this problem is to use dimensional analysis. We are given a mass and two densities.rnThen to get volume just invert the densities and multiply by the mass. The difference between the two densities is nearly one.rnrn300/1.11~300 $\Rightarrow$ D)270

Reply to this comment

anmuhich
2009-03-15 12:22:06

Right I agree with NaijaProfessor. It's just a sum of the forces acting upon the balloon. The bouyant force is the weight displaced by the balloon due to Archimedes principle. This bouyant force equals the weight of the helium plus the weight of the mass. Solving this equation for the volume gives you 270. This amounts to the same thing as what Joe is saying but this is why it works. It's good that many people had the intuition to subtract the densities. If all else fails on this test it's best to go with your intuition.

Reply to this comment

greenfruit
2008-11-05 08:41:46

It's really simple, conceptually. For the balloon to float:

The mass of the block + the mass of the He in the balloon < the mass of the air displaced by the balloon

300kg + (x * .18 kg/m^3) <= x * 1.29 kg/m^3

with x being the volume of the balloon.

Solve for x, x=270 m^3.

Reply to this comment

duckduck_85
2008-10-31 17:58:16

I don't get why the buoyant force uses the volume of He while using the density of air. Isn't it supposed to be equal to the mass of the fluid displaced? Naturally, air by itself can't lift the balloon, but i just don't get the reasoning. Please help.

Reply to this comment

grae313
2007-11-01 13:44:05

It looks like there is some confusion because the problem says, "neglect the mass of the balloon," but by this it means to neglect the mass of whatever material encloses the helium, not the helium itself as Yosun has assumed.

Thank you for this site, Yosun!

Reply to this comment

joe
2006-10-21 21:03:19

One could also find the difference in the densities of air and helium (1.29-0.18=1.11) Then use that number to find the answer (300/1.11=270).

jesford
2008-04-05 10:13:47

I agree with joe... the correct way to do this problem would be to use the differences in densities for finding the bouyant force.

I really appreciate this site! Thanks Yosun, and everyone who contributes!

Poop Loops
2008-11-01 19:49:22

That's the way I did it. I thought it was dubious reasoning, but if others did it the same way then it must be alright to do it that way.

QM320
2008-11-05 20:59:29

That's what I did as well. I figured that the buoyancy force (up) of the He must equal the sum of weight + the downward force exerted by the air. I took the downward force exerted by the air to be 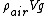$\rho_{air}Vg$ where V is the volume of helium (assumed to be approximately equal to the volume of air exerting the force).

carl_the_sagan
2008-11-07 19:42:52

Also did it this way, if you can see a quick trick like this and arrived at a supplied answer, it's almost always a good thing.

jmason86
2009-07-12 15:47:58

I also did it like this.
It didn't seem like there should be any fundamental constants coming into play for this problem, so I just did dimensional analysis to figure out what combination of the values given would yield 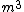$m^3$ units. It worked out and only took about 30 seconds to complete the entire problem.. important time saved on this test :)

Reply to this comment

joe
2006-10-21 21:01:53

Reply to this comment

NaijaProfessor
2005-11-24 06:18:47

If u equate the buoyant force to the weigth of the mass and that of helium, ur answer will be very approximate to 270m3. The helium gas does have weight u know acting downwards. Thus,

0.189Vg + 300g = Bouyant force

Reply to this comment

Bare Basic LaTeX Rosetta Stone