|
GR0177 #52
|
|
|
Problem
|
|
|
This problem is still being typed. |
Advanced Topics }Solid State Physics }Solid State Physics
Recall the definition of a primitive cell to be the unit cell divided by the number of lattice points in a Bravais lattice. A Bravais lattice is just a lattice that looks isotropic from any point---everywhere the same no matter the point-perspective.
Simple cubic has 1 lattice point to generate its Bravais lattice.
Body-centered cubic has 2 lattice points to generate its Bravais lattice. (One can keep on tesselating the a lattice point on one corner and the lattice point on the body center to generate the whole BCC lattice.)
Face-centered cubic has 4 lattice points to generate its Bravais lattice. (One can keep on tesselating the lattice point on each face surrounding a corner lattice point.)
So, anyway, from the above, one finds choice (C) for BCC's unit cell.
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Poop Loops
2008-11-01 19:42:37 | I'm in Solid State physics now, 6th week, we did all this stuff, and I still couldn't understand the question. Jesus Christ, I REALLY hate Solid State.
f4hy
2009-04-02 16:53:09 |
Totally with you on that.
|
ali8
2013-10-04 15:22:35 |
I've already done SSP 1, and I can tell you that I agree, the crystal structure thing is ugly, but the rest is nice.
|
|  | Sadjar
2007-10-29 16:02:35 | This problem is actually really simply. The way a primitive cell is defined in Solid State Physics is a certain Volume which, without overlap or leaving gaps, can cover the entirety of the solid if used as a bricks/building blocks. Also, they must have a lattice point density of 1 (in other words, they can only contain 1 lattice point).
The methodical way of doing this is first calculating the lattice point density of a BCC lattice:
Each of the 8 corner lattice points are shared between 8 unit cells each (4 unit cells under, 4 over, draw it, it makes more sense to look at it). And the center lattice point belongs entirely to each of the unit cells. So the density of lattice points per unit cell is 8*(1/8)+1*1=2.
So if the density of lattice points in an unit cell is 2 and the volume of an unit cell is a^3, it follows that we can construct a volume of (a^3)/2 which will contain only ONE lattice point (namely a primitive unit cell volume by definition).
This can be done really fast if you simply remember the lattice point densities of some basic lattices like Body centered and Face centered and Diamond.
Note: Face centered lattice has a density of 4 (try to calculate it) |  | Richard
2007-10-25 23:27:44 | I don't know much about solid state physics, Yosun, but I think your solution here is a bit obfuscated.
A Bravais lattice is just an infinite lattice that is expressible in terms of a finite number of defining "primitive vectors." Then, the "primitive unit cell" is the smallest volume that can be used to span that infinite lattice.
Clearly, the tetragonal cell displayed is not the primitive cell. This rules out (D).
My thing is, why isn't it 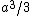 , the volume created by two square pyramids each with volume , the volume created by two square pyramids each with volume 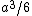 ? What am I missing here? ? What am I missing here?
( I never got to take a solid state class...)
I think 12% got this one right.
|  | Hoffman1512
2007-10-03 21:20:34 | As far as I know, the primitive unit cell volume for these structures is much simpler. If one takes the unit cell volume 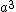 for all three mentioned structures, and divides by the number of atoms/molecules in the unit cell one obtains the volume of the primitive unit cell. Thus, for all three mentioned structures, and divides by the number of atoms/molecules in the unit cell one obtains the volume of the primitive unit cell. Thus,
number of atoms in simple cubic (SC): 1
-- from each corner for 8 corners from each corner for 8 corners
number of atoms in body-centered (BCC): 2
--SC plus one atom in center
number of atoms in face-centered (FCC): 4
--SC plus  atom on each of six faces atom on each of six faces
In this particular problem:

which is answer (C).
carl_the_sagan
2008-11-07 19:32:58 |
This explanation makes by far the most sense to me. Though I never took a solid state course, I recall this from the bit we got to in modern and condensed matter lab.
|
yummyhat
2017-10-26 16:48:17 |
best answer
|
|  | KarstenChu
2007-03-22 18:08:18 | Ok, since I'm a physics noob and too lazy to look up the word tesselate, here's how I figured it out. The primitive unit cell is defined by three primitive vectors...and you need to pick these primitive vectors in a way that you can access each lattice point through a combination of these vectors. Thus I picked the two base vectors and the vector to the body centered point. A little geometry and whammo.
maxdp
2013-10-18 11:28:05 |
I tried this method and it gave me an entirely wrong answer (a^3/12). I assumed that we would want the volume of the shape made by the primitive vectors, which would be a small tetrahedron. If someone could explain a way to understand this problem geometrically (similar to what Karsten is trying to do), that'd be really helpful. I understand the shortcut way of dividing the total volume by the number of lattice points, but I'm really craving a geometric argument that's more intuitive.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
