|
GR0177 #51
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Almno10
2010-11-09 12:39:51 | The "one half rule" (in basic physics II texts) states that the intensity of light emerging from a single sheet is I' = (1/2)Io. The cosine rule gives the rest.
True, the original solution is incorrect - you do not square the previous intensity, only the cosine. Squaring the intensities throughout would give an answer of 1/128*Io! Thats not good. |  | davidkaleko
2010-09-15 13:40:57 | You could also note that the max amount of light intensity through a polarizer is 1/2 of the initial intensity. In this case, angles ignored, the maximum light allowed through is (1/2)(1/2)(1/2) the initial intensity, or Io/8. Options C, D, and E are greater than this maximum, and since each polarizer is only 45 degrees apart from the previous, the intensity will never drop to zero. Thus, B is right.
Crand0r
2010-11-10 18:57:24 |
This is not right. If the angle is 0, all the light passes through (ignoring deviations from the ideal polarizer).
|
|  | jmason86
2009-07-03 14:27:44 | Conceptually this is really weird.
The first filter cuts the light in half, which makes sense. You could imagine that all the light is now, say, vertical.
The second filter is at 45 degrees, but the light is already vertical, so this should just reduce the intensity.
The last filter is at 90 degrees from the first, so it should only allow horizontal light through, but there is none... it's all vertical. So I would expect no light to be transmitted through this filter.
The math works out fine, but I cant imagine how this works physically.
kroner
2009-10-06 14:57:02 |
One way to think about it is in terms of photon spin. If you have an ensemble of photons in a pure vertical spin state and you measure the spin in the 45 degree orientation, the act of measuring messes up the vertical/horizontal state. After that if you measure the vertical/horizontal orientation you'll get half and half.
|
|  | Richard
2007-10-25 22:41:25 | This is another instance of Malus' Law:
When you have polarized light 
through a polarizer at an angle  , ,
) gets through. gets through.
How to get the first 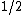 : :
Initially, however, the light is unpolarized.
You might just realize that 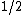 of the unpolarized light gets through, but a more justifiable approach is to of the unpolarized light gets through, but a more justifiable approach is to
imagine a superposition of light more or less polarized equally at every possible angle (unpolarized light):
Apply Malus' Law to this situation and you get
+\frac{I_0}{N}cos^2 (\theta_2)+...\frac{I_0}{N}cos^2 (\theta_N)) which is nothing more than the average of which is nothing more than the average of =1/2) . . |  | antithesis
2007-10-01 13:26:55 | I understand the math here, but intuitively, something seems off:
If you were to take out the second polarizer, the 3rd would be 90 degrees from the first, and you would get
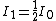 and and 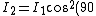 = 0) . .
So how come adding the second polarizer now allows light to go through?
irishroogie
2007-10-02 11:22:33 |
You have to consider the angle between the 2nd and the 3rd polarizer which is 45 degrees.
|
f4hy
2009-04-02 16:50:57 |
Yes this is the mystery of it. It seems like light should not make it through but it does!
|
ifprado
2015-10-25 23:35:43 |
Because of the superposition principle of quantum mechanics. [guessing, not actually sure].
|
|  | Andresito
2006-03-08 22:10:28 | Intensity is not squared but only the cosine function. Otherwise the dimensions would not be correct.
Thanks for working out the solutions Yosun :p |  | kk7t
2005-12-10 11:25:41 | there should be a square on I1, I2. |  |
|
| Post A Comment! |
You are replying to:
You could also note that the max amount of light intensity through a polarizer is 1/2 of the initial intensity. In this case, angles ignored, the maximum light allowed through is (1/2)(1/2)(1/2) the initial intensity, or Io/8. Options C, D, and E are greater than this maximum, and since each polarizer is only 45 degrees apart from the previous, the intensity will never drop to zero. Thus, B is right.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
