|
GR0177 #50
|
|
|
Problem
|
|
|
This problem is still being typed. |
Wave Phenomena }Sound }Sound
Since the wavelength of the wave does not change, as the pipe presumably stays approximately the same length, only the frequency varies. If the speed of sound changes, then the frequency changes. If the speed of sound is lower than usual, then the frequency is lower. Thus, choices (A), (B) and (C) remain. Calculate 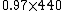 to get choice (B). to get choice (B).
|
|
|
Alternate Solutions |
uhurulol
2014-10-20 18:24:42 | If you're looking for a more mathematical answer, use the simple relation
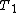 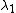 = = 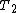 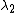
Note that  is just is just 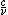 , and as such , and as such
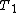 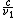 = = 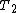 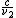 . .
 cancels on both sides and cancels on both sides and 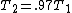 , so plugging everything in and cancelling , so plugging everything in and cancelling 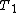 we have we have
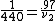
Cross multiply to obtain 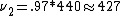 , as in choice (B). Hope this helps. , as in choice (B). Hope this helps. |  | dham
2010-10-06 23:07:59 | For a quick guess: Cold instruments go flat. (Frequency goes down), leaving choices A-C.
Directly: c= f, so speed of sound is directly proportional to wavelength. f, so speed of sound is directly proportional to wavelength.
Find the change in wavelength by finding 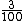 (440)=3*4.4. (440)=3*4.4.
That's little over 12.
440-12=428, which is a little over 427 (B).
B is the right answer. |  |
|
|
Comments |
star19
2019-08-13 10:33:05 | Nice blog, the article you have shared is good.\r\ntest\r\n |  | star19
2019-08-13 10:30:46 | Nice blog, the article you have shared is good.This article is very useful. My friend suggest me to use this blog.\r\ntest |  | star19
2019-08-13 10:27:32 | Our academic pursuits, along with a range of extracurricular activities, help in honing a child\'s skills and ensuring that he/she grows to be a mature and responsible citizen.
\r\nbest " target="_blank">http://www.gdgoenkanoida.edu.in\">best school in greater noida\r\n\r\n
SofiaStirling
2019-12-21 22:38:06 |
\r\naustralian assignment help\r\n\r\n\r\n[URL=https://my-assignment.help/]australian assignment help[/URL]\r\n\r\n\r\n[myassignmenthelp australia](https://my-assignment.help/)\r\n\r\n\r\n[url=https://my-assignment.help/accounting-assignment-help/]https://my-assignment.help/accounting-assignment-help/[/url]\r\n\r\n\r\n\"weblink\":https://icasinoreviews.info/gaming-club-casino-nz/\r\n\r\n[http://www.edgewall.com/ Edgewall Software]\r\n\r\nwrite my essay reviews
|
|  | yummyhat
2017-10-26 12:40:36 | use the fact that wavelength*frequency=velocity. notice that the wavelength is determined by the pipe and is constant. use a ratio because the ratio of velocities is already given, and solve for the final frequency. |  | kevintah
2015-10-05 10:05:11 | Hey guys, . . . . Kevin Tah Njokom here :)\r\n\r\n Currently studying for the Physics GRE. This is my first response here. I think it is how to attack the problem, although you have to be able to do it fast to account for time. So here goes.\r\n First a few observations. I noticed that the solution was given by @uhurulol using some very quick method, which is probably faster. My solution is an alternative way of arriving at the answer.\r\n\r\n Notice that the pipe is open at one end. This makes the following relation valid. 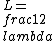 . Here L is the length of the pipe . This is a good thing because we know that the length is not suddenly going to change. \r\n We also know the relation that . Here L is the length of the pipe . This is a good thing because we know that the length is not suddenly going to change. \r\n We also know the relation that 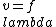 . \r\n We solve for . \r\n We solve for 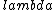 from this, and then substitute the value into the equation for from this, and then substitute the value into the equation for 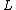 . This gives us . This gives us  . Since . Since 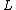 is constant it mus apply for the new and old frequency and velocity.\r\n\r\n It is mentioned that on a cold day, the speed of sound is 3% lower than it would be at 20 degrees.\r\n\r\n This means is constant it mus apply for the new and old frequency and velocity.\r\n\r\n It is mentioned that on a cold day, the speed of sound is 3% lower than it would be at 20 degrees.\r\n\r\n This means  \r\n \r\nThis makes \r\n \r\nThis makes 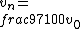 \r\n\r\nThus:\r\n\r\n \r\n\r\nThus:\r\n\r\n 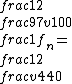 \r\n\r\nWhen you crunch things out, you get 426.8 close to 427. This makes B, the answer.\r\n\r\n Good Luck on the Physics GRE everyone. Study hard. Let me know what you think of my answer. \r\n\r\nWhen you crunch things out, you get 426.8 close to 427. This makes B, the answer.\r\n\r\n Good Luck on the Physics GRE everyone. Study hard. Let me know what you think of my answer.
kevintah
2015-10-05 23:39:49 |
Some how the Latex got distorted, and I can\'t edit it . Oh well
|
|  | uhurulol
2014-10-20 18:24:42 | If you're looking for a more mathematical answer, use the simple relation
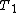 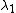 = = 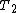 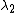
Note that  is just is just 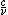 , and as such , and as such
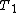 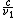 = = 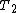 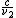 . .
 cancels on both sides and cancels on both sides and 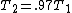 , so plugging everything in and cancelling , so plugging everything in and cancelling 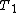 we have we have
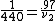
Cross multiply to obtain 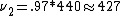 , as in choice (B). Hope this helps. , as in choice (B). Hope this helps. |  | jwbrooks0
2014-09-22 21:21:30 | I'm confused. The speed of sound should be proportional to the sqrt(T). http://en.wikipedia.org/wiki/Speed_of_sound#Speed_in_ideal_gases_and_in_air
Therefore, why isn't 440*sqrt(0.97) = 433 correct?
Stardust
2015-10-22 15:37:18 |
The question says the \'SPEED OF SOUND is 3% lower than...\' not the temperature.
|
|  | dham
2010-10-06 23:07:59 | For a quick guess: Cold instruments go flat. (Frequency goes down), leaving choices A-C.
Directly: c= f, so speed of sound is directly proportional to wavelength. f, so speed of sound is directly proportional to wavelength.
Find the change in wavelength by finding 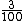 (440)=3*4.4. (440)=3*4.4.
That's little over 12.
440-12=428, which is a little over 427 (B).
B is the right answer. |  | f4hy
2009-11-06 23:27:57 | They give you the 20 degrees as a trick then?
dham
2010-10-06 23:09:25 |
Not really, it's just an initial condition.
|
|  | michealmas
2006-12-30 11:48:37 | use the 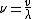 equation relating freq., velocity, and wavelength. equation relating freq., velocity, and wavelength. |  | nahmad
2006-03-30 22:21:27 | One quick way of doing this calculation in your head is to consider it as a 3% loss. Thus -3 for every 100, which gives a loss of -12. 440-12 = 428. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
