|
GR0177 #4
|
|
|
|
|
Alternate Solutions |
amber
2014-10-22 15:11:44 | Look at the problem thru Center of Mass
Again find the velocity of CM which equals the initial and final velocities of each mass
V = m1v1/ m1+m2 = 2v1/3 = v_final
set the ratio KEf/KEi
0.5 3m 4v1^2/9 / 0.5 2m v1^2 = 2/3
Then 1 - 2/3 to get the energy lost 1/3 |  | secretempire1
2012-08-28 06:47:39 | Formula for kinetic energy 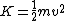
Let 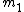 and and 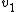 correspond to the mass and velocity of block 1, correspond to the mass and velocity of block 1, 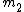 and and  for block 2, and for block 2, and 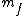 and and 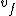 for the resultant combined mass block, where for the resultant combined mass block, where 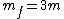 . .
Total initial kinetic energy 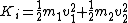
Since 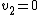 , , 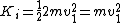
Total final kinetic energy 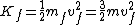
Performing the same operation for momentum:
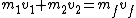
Solving for 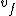 will yield will yield 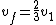
Plug this into the equation for final kinetic energy, and you get 
This implies that 1/3 of the energy is lost. |  |
|
|
Comments |
Nebula
2015-09-18 20:50:37 | Don\'t misread this question and think they are asking for the ratio of final kinetic energy to initial kinetic energy, in which you would get answer (E) 2/3. Easy points lost. |  | amber
2014-10-22 15:11:44 | Look at the problem thru Center of Mass
Again find the velocity of CM which equals the initial and final velocities of each mass
V = m1v1/ m1+m2 = 2v1/3 = v_final
set the ratio KEf/KEi
0.5 3m 4v1^2/9 / 0.5 2m v1^2 = 2/3
Then 1 - 2/3 to get the energy lost 1/3 |  | Dax Feliz
2012-11-06 22:03:16 | Does any one know why we subtract the ratio from 1 to get the fractional loss of energy? I think I missed something here... |  | CortunaMJM
2012-10-09 02:40:13 | how to get the initial kinetic energy if there's no velocity given?
ezfzx
2012-10-13 17:48:25 |
Since the problem is only looking for a RATIO of energy, the velocity is not needed.
|
|  | secretempire1
2012-08-28 06:47:39 | Formula for kinetic energy 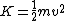
Let 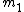 and and 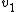 correspond to the mass and velocity of block 1, correspond to the mass and velocity of block 1, 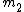 and and  for block 2, and for block 2, and 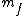 and and 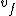 for the resultant combined mass block, where for the resultant combined mass block, where 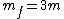 . .
Total initial kinetic energy 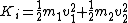
Since 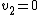 , , 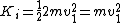
Total final kinetic energy 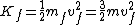
Performing the same operation for momentum:
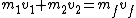
Solving for 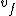 will yield will yield 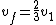
Plug this into the equation for final kinetic energy, and you get 
This implies that 1/3 of the energy is lost. |  | thesandrus86
2011-04-24 14:21:41 | por conservación del momento tenemos:
2mVi+mVi=(m+2m)Vf
2m =3mVf
Vf= 2/3.... |  | archard
2010-04-11 14:54:59 | Another quick way is to remember that kinetic energy can be written as 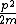 , and since momentum is conserved, the final:initial kinetic energy ratio is , and since momentum is conserved, the final:initial kinetic energy ratio is }{2(m1+m2)}) = =  . Which means the fractional kinetic energy loss is . Which means the fractional kinetic energy loss is 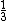 |  | wittensdog
2009-10-08 16:29:07 | Here's something that's surprisingly useful. When a moving body hits a second one at rest, and they stick, the fractional loss of kinetic energy is,
m2 / ( m1 + m2)
If you just memorize that, all sorts of problems involving sticky collisions become way faster, even ones where you have falling masses on pendulums and so forth.
Dhananjay
2013-05-30 00:26:45 |
is m2 the mass of the moving ball or the ball at rest?
|
|  | herrphysik
2006-09-19 16:14:15 | Small typo: You're missing a 2 in the left side of the initial KE equation. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
