GREPhysics.NET: GR0177 #38

GR0177 #38

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Electromagnetism $\Rightarrow$ }AC Circuit

The current is maximized when one has resonance. Resonance occurs when the complex impedance is 0, or when 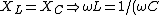$X_L=X_C \Rightarrow \omega L = 1/(\omega C)$ . Plug stuff in to get choice (D).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

giga17
2010-08-11 02:06:05

This is one of those problems where dimensional analysis would help a lot. The only way to get a time scale out of the physical quantities from R, L and C is 1/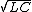 $\sqrt{LC}$ .

acukierm
2013-09-23 19:41:23

$RC$ also has units of time. So pure dimensional analysis with no other information (e.g., that the inductor is important for finding the resonance frequency while the resistor is not) would not work here.

Reply to this comment

zmb_hep
2009-09-08 15:36:21

One can also use the resonant frequency condition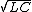 $\omega_0$ =1/ $\sqrt{LC}$ .

We are given that $\omega_0$ =10^3 , and that L=25 mH, plugging these values in and solving for C also gives the correct answer

dberger8
2016-01-15 22:14:52

We\\\\\\\'re given the driving frequency, not the natural frequency.

jfcdu
2018-07-15 14:40:57

@dberger8\\\\r\\\\n the idea, is that the driving frequency is set by the problem. If we want to maximize the amplitude of the current, we need to pick C such that the resonant frequency *is* the driving frequency. Thus we can set 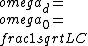$\\\\\\\\omega_d = \\\\\\\\omega_0 = \\\\\\\\frac{1}{\\\\\\\\sqrt{LC}}$ and solve for C.

jfcdu
2018-07-15 14:43:27

@dberger8 the idea is that the driving frequency is set by the problem. If we want to maximize the amplitude of the current, we need to pick C such that the resonant frequency *is* the driving frequency. Thus we can set 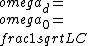$\\omega_d = \\omega_0 = \\frac{1}{\\sqrt{LC}}$ and solve for C.

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone