|
GR0177 #19
|
|
|
Problem
|
|
|
This problem is still being typed. |
Advanced Topics }Astrophysics }Astrophysics
It takes 4 H's to create a Helium nucleus in the sun's primary thermonuclear reactions. One either remembers this or can derive it from conservation of mass. The atomic mass of Hydrogen is 1 (since it has just 1 proton), while the atomic mass of Helium is 2 (2 protons, 2 neutrons).
|
|
|
Alternate Solutions |
bostroem
2013-01-15 20:11:10 | proton-proton cycle:
First this happens twice:
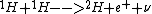
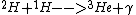
Then
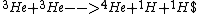 |  | GREview
2009-05-19 15:28:49 | Fusion in the Sun is governed by 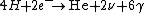 (with (with 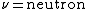 and and 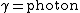 ). Thus, the mass difference between the products and reactants is the difference between the He atom and the 4 H atoms. ). Thus, the mass difference between the products and reactants is the difference between the He atom and the 4 H atoms. |  |
|
|
Comments |
bostroem
2013-01-15 20:11:10 | proton-proton cycle:
First this happens twice:
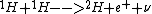
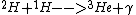
Then
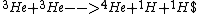 |  | betelguese05
2012-10-11 14:26:27 | This wasn't a choice, but I'm interested. In magnetic confinement fusion, the reaction at play is pretty exclusively Deuterium + Tritium -> He + n. Is this possible in the sun? I imagine the cross section would be much higher since only two particles have to collide, but the sun may have very little deuterium and tritium.
Giubenez
2014-10-22 02:27:51 |
The reaction
Deu + Trit -> 4He + n
has a bigger cross section at the temperature that is possible to achieve in a magnetic confined plasma (10-20keV). At 100keV its cross section is 100 times bigger than D-D or D-He3. At lower temperature the difference is greater, (20kev more than 3ODG) but at 1MeV their cross section is similar. That's why D-D is used in in H-bombs and in the sun and also why D-T is easier to exploit in lab.
Furthermore D-D reaction gives only about 3MeV whereas D-T gives more than 17MeV...
Moreover Tritium has a mean life of 12years and thus it's only a transient or a secondary reaction in the sun.
|
|  | torturedbabycow
2010-04-01 17:04:16 | "The sun is a mass of incandescent gas, it's a giant nuclear furnace, where hydrogen is built into helium at a temperature of millions of degrees..."
Now all you have to remember is that the mass of one helium nucleus is about four times the mass of one hydrogen nucleus, and voila, (B). ^___^ |  | physicsman
2010-01-19 15:38:59 | Qualitatively: 1 proton + 1 electron is needed for every neutron
simply accounting for all the constituents of helium by pulling them from hydrogen will give you the proper number of hydrogen atoms to use. |  | GREview
2009-05-19 15:28:49 | Fusion in the Sun is governed by 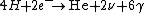 (with (with 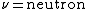 and and 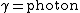 ). Thus, the mass difference between the products and reactants is the difference between the He atom and the 4 H atoms. ). Thus, the mass difference between the products and reactants is the difference between the He atom and the 4 H atoms.
torturedbabycow
2010-04-01 17:05:53 |
I think you mean neutrino, not neutron!
|
dinoco
2010-11-10 07:49:05 |
it should be 
|
|  | GREview
2009-05-19 15:28:13 | Fusion in the Sun is governed by 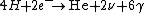 (with (with 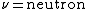 and and 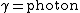 ). Thus, the mass difference between the products and reactants is the difference between the He atom and the 4 H atoms. ). Thus, the mass difference between the products and reactants is the difference between the He atom and the 4 H atoms. |  | bpat
2007-11-01 19:03:51 | I think it is a little more complicated than that, since 4*H does not equal 1*He. I think you just have to memorize the pp cycle for solar sized stars*.
*I guess they could have been really mean and said it was a very massive star. Then the answer would have been CNO cycle, not pp. |  | T
2005-11-10 20:03:39 | small typo there, atomic mass of He is 4 |  | T
2005-11-10 20:03:02 | |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
