|
GR0177 #100
|
|
|
Problem
|
|
|
This problem is still being typed. |
Optics }Interferometer }Interferometer
This is a nice problem.
An interferometer, like its name suggests, has to do with interference. Namely, it splits light-beams through the beam-splitters (BS) half and half, then recombines them at the end---the end result shows interference which varies depending on whether the moveable mirror is placed a quarter of a wavelength away (so that the path difference, which is twice that, is half a wavelength).
A fringeshift occurs whenever 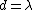 . Thus . Thus 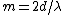 , where m is the number of fringes and , where m is the number of fringes and  is the wavelength. is the wavelength.
Using the information for the red beam, one can find 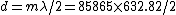 . Applying the same equation for the green beam, one finds that . Applying the same equation for the green beam, one finds that 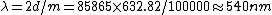 , as in choice (B). , as in choice (B).
|
|
|
Alternate Solutions |
Barney
2012-11-09 12:43:13 | Here are solutions I found on google for the 2008 test:
http://physicsworks.files.wordpress.com/2012/09/gr0877_solutions.pdf |  | bootstrap
2007-04-06 22:12:39 | This is very easy and requires a little intuition, but no equations. Violet light is in the 400 nm. Red is in the 700nm - 600nm (600 nm is a orange-red). Anything not between 400nm-700nm is something we cant see, so therefore not D or E. C is close to 600 nm, so thats out. Therefore we have 2 answers left. Simple knowing that green is about 550nm will give you the answer. Also using ROYGBIV will sugest that 500nm answer is entering the blue range. |  | bterranova
2006-06-19 10:02:36 | There is a much simpler solution. The ratio between the number of fringes and wavelengths must be equal between the two sources, so: 100,000/(\lambda) = 85,865/632.82 gives you the solution in nm.
rizkibizniz
2011-10-21 02:21:39 |
I am here to CONFORM that bterranova's both method and answer is WRONG. BAD PHYSICS!
Think about it. If you move the mirror by 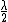 , that means the total distance the light has to travel is changed by twice , that means the total distance the light has to travel is changed by twice 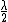 , (TO the mirror, and FROM the mirror) ie. the distance change is , (TO the mirror, and FROM the mirror) ie. the distance change is  , which corresponds to , which corresponds to 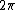 phase change, ie ONE fringe. phase change, ie ONE fringe.
so the correct equation for a simple Michelson interferometer : 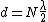 , ,
where N is the number of fringes, d is the distance the mirror has moved,  is the wavelength. is the wavelength.
now the CORRECT ratio is,
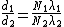
since 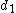 = = 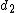 , ,
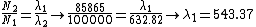
|
|  |
|
|
Comments |
Barney
2012-11-09 12:43:13 | Here are solutions I found on google for the 2008 test:
http://physicsworks.files.wordpress.com/2012/09/gr0877_solutions.pdf
gbenga
2014-10-19 06:31:21 |
And here're the 08' questions: http://www.ets.org/s/gre/pdf/practice_book_physics.pdf
|
|  | dinoco
2010-11-13 22:22:18 | Or you can recall your days as a researcher in the optics lab working on a Lidar that used green lasers of 546nm. |  | tjrelic
2010-10-08 14:21:02 | I used bterranova's solution as well and it gives the right answer.
85865*632.8 = G*100000
Some rounding because #100 AHHH time is running out...
G~632.8*8.6/10
G~544
Anyway, test is tomorrow, and man am I ill prepared. Don't procrastinate like me! Study for three months an hour a day! |  | iamSMRT
2009-11-07 00:47:29 | I did this with a simple ratio
633 nm * 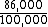 and you get approximately 540 nm. and you get approximately 540 nm. |  | dhruv
2009-10-25 07:12:44 | What is the resolution of Michelson interferrometer with wavelength 640nm ?? |  | ashwinat884
2008-11-07 11:59:19 | Thanks a lot Yosun.
|  | Imperate
2008-09-04 05:45:02 | I thought the formula was }{\lambda} ) implying fringe maxima occur when implying fringe maxima occur when 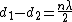 .Assuming .Assuming 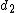 (the vertical distance) is constant, this implies that (the vertical distance) is constant, this implies that 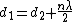 , i.e. everytime you move , i.e. everytime you move 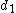 through through 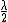 you get another maxima. This surely implies the fringes are seperated by you get another maxima. This surely implies the fringes are seperated by 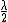 .rnrnSo if for red light you get 100,000 fringes after moving a distance d, this implies .rnrnSo if for red light you get 100,000 fringes after moving a distance d, this implies 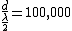 . Since we are given the wavelength of red as 632.82 we can solve for d, and obtain d=0.0316m. rnNow using the same formula for the green case: . Since we are given the wavelength of red as 632.82 we can solve for d, and obtain d=0.0316m. rnNow using the same formula for the green case: 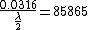 , solving for the wavelength one finds that the green wavelength is 736.99nm exactly.rnrnWhich concerns me since obviously red light should have longer wavelength than green, don't understand where I have gone wrong though. , solving for the wavelength one finds that the green wavelength is 736.99nm exactly.rnrnWhich concerns me since obviously red light should have longer wavelength than green, don't understand where I have gone wrong though.
Imperate
2008-09-04 06:03:37 |
oops sorry, I just reread the 100,000 corresponds to the number of green fringes 85865 to the number of red, everything works perfectly.
for red:
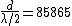 and since wavelength=632.82nm this implies that d=0.02716m and since wavelength=632.82nm this implies that d=0.02716m
for green:
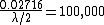 , which solving for the wavelength gives 543.37nm as in choice (B). , which solving for the wavelength gives 543.37nm as in choice (B).
I think way to deduce this, would be rule out (D) and (E) immediatley since we know green wavelenth must be shorter. ROYGBIV. Then simply to look at the ratio of either 100000/85865 or 85865/100000, the former is greater than one so is going to give a bigger wavelength and thus we can throw this away in favour of the latter.
The ratio of the two formulas leads to:
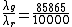 thus implying that the green wavelength is approximatley 85% the red wavelength thus implying that the green wavelength is approximatley 85% the red wavelength
|
|  | Richard
2007-10-31 09:10:34 | Yosun,
Do you mean to say that a fringe shift occurs
when 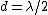 ? ?
A fringe shift occurs when the light is displaced a total distance  . Since it has to make a round trip, this is when . Since it has to make a round trip, this is when 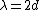 , or generally when , or generally when 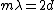 . .
greenfruit
2008-11-06 07:45:06 |
you're right that a fringe shift occurs whenever d is a multiple of  /2 /2
but, she somehow ends up with the correct formula: m = 2d/
|
Nezumi
2012-02-10 12:41:30 |
@greenfruit,
You said "you're right that a fringe shift occurs whenever d is a multiple of 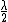 " "
which is:
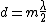
solve for 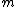 : :
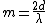
|
|  | bootstrap
2007-04-06 22:12:39 | This is very easy and requires a little intuition, but no equations. Violet light is in the 400 nm. Red is in the 700nm - 600nm (600 nm is a orange-red). Anything not between 400nm-700nm is something we cant see, so therefore not D or E. C is close to 600 nm, so thats out. Therefore we have 2 answers left. Simple knowing that green is about 550nm will give you the answer. Also using ROYGBIV will sugest that 500nm answer is entering the blue range.
bootstrap
2007-04-13 15:26:45 |
Note in problem 69, on this test they tell you the blue light is 480nm and in this problem red light is 632nm. With this information provided for ETS then it further suggests that C is the answer.
|
|  | jitin1984
2006-10-27 14:07:24 | hey watz up to begin iam a BE undergrad shifting to engineering physics.
any ways i just wanna know from where do i study error analysis. if any one has the notes on the comp plz mail them to me.
also if any one has practice problems (except for the four papers and two small other ones) specially for phy gre plz i want the soft copy.
bye, best of luck to everyone |  | bterranova
2006-06-19 10:02:36 | There is a much simpler solution. The ratio between the number of fringes and wavelengths must be equal between the two sources, so: 100,000/(\lambda) = 85,865/632.82 gives you the solution in nm.
Blake7
2007-09-22 06:41:21 |
Depending on how much thought processing one has left upon encountering Question 100, one might also take the perspective that
85865 is to 100,000 as 632.82 is to green and then subtract just shy of 15% (restaurant tip calculation; move the decimal point left and add in half of that) from 633 to get "pretty nearly" (B).
What a nice, safe, forgiving problem!
(Now go back and pick up some more points that you skipped over the 1st time through!)
|
blah22
2008-04-07 10:47:32 |
Just me or is this completely wrong? I get ~740 when I use this method.
I think the correct ratio is 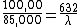
|
AER
2009-04-02 18:55:40 |
I think this gets you about 740nm, as in D)
|
natestree
2011-03-07 16:54:08 |
Is it just me...or is the math in this problem annoying to do without a calculator...which we cant have on the test....
|
mistaj
2011-08-24 09:53:19 |
This ratio isn't correct, it gives you D. Solving for  , , 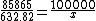 . So, . So, 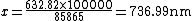 . Which is D and is incorrect. . Which is D and is incorrect.
The correct form is 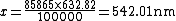 , which gives you (almos) B in nm. This is because , which gives you (almos) B in nm. This is because 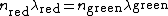 . .
|
rizkibizniz
2011-10-21 02:21:39 |
I am here to CONFORM that bterranova's both method and answer is WRONG. BAD PHYSICS!
Think about it. If you move the mirror by 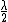 , that means the total distance the light has to travel is changed by twice , that means the total distance the light has to travel is changed by twice 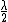 , (TO the mirror, and FROM the mirror) ie. the distance change is , (TO the mirror, and FROM the mirror) ie. the distance change is  , which corresponds to , which corresponds to 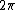 phase change, ie ONE fringe. phase change, ie ONE fringe.
so the correct equation for a simple Michelson interferometer : 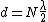 , ,
where N is the number of fringes, d is the distance the mirror has moved,  is the wavelength. is the wavelength.
now the CORRECT ratio is,
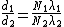
since 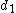 = = 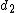 , ,
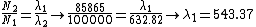
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
