|
GR9677 #77
|
|
|
|
|
Comments |
NeuralLotus
2014-09-26 19:22:40 | The problem I am facing with this question is that if S1=S2, then B gives, H = -2JS1(S1+1/2). But, in this case, you should have H= -JS1(S1+1), since S1^2 = S1(S1+1). None of the answers fit this constraint, though. Well, besides the trivial answer, A, assuming which, you'd have to assume that S1 is always 0, in which case S2 is as well. |  | mpdude8
2012-04-20 18:13:30 | I looked at this problem, and said, there must be elimination. No way I have time to do any algebra.
A is gone. E is gone, there's no division anywhere here. C is gone, taking the dot product is way more complicated than that.
B was an interesting choice, but on the basis of where the ions were "fixed", I picked D. |  | KanHengLee
2011-10-10 02:34:18 | I am really confused with the official answer.
In the last step (A+B)^2 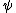 = (A+B)(A+B+1) = (A+B)(A+B+1)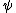
is used. However, is that valid?
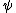 is the eigenfunction of both S1^2, S2^2, is the eigenfunction of both S1^2, S2^2,
but is it so for (S1+S2)^2?
I don't know how to prove that [(S1+S2)^2, S1^2]=0.
If I think in a wrong way, please help me!!!!
wavicle
2011-10-13 13:42:28 |
The point of this problem is that we don't know the eigenvalue of 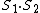 . We do however know the . We do however know the 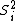 . Using the identityrnrn . Using the identityrnrn^2 = S_1^2 + S_2^2 + 2S_1 \cdot S_2) rn rn^2 - S_1^2 - S_2^2 = S_1 \cdot S_2) rnrnThe leap I believe you're supposed to make is that the eigenvalue of rnrnThe leap I believe you're supposed to make is that the eigenvalue of ^2) is is (S_1 + S_2 + 1)) which is the same as the other eigenvalues replacing the which is the same as the other eigenvalues replacing the 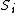 with with 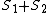 rnrnSee also reply by 99percent to astro regarding sameness of (B) and (D)rnrnI suppose the lesson here is, always chose the unsimplified version of the answer? rnrnSee also reply by 99percent to astro regarding sameness of (B) and (D)rnrnI suppose the lesson here is, always chose the unsimplified version of the answer?
|
|  | keradeek
2011-09-23 00:41:27 | The lowest energy state will be when the two ions have their angular momentum vectors most appositely aligned. That happens when m_z of ion 1 is S_1, and m_z of ion 2 is -S_2. Thus the answer is B, which is the same as D, so this question has two answers.
keradeek
2011-09-23 01:54:31 |
(forgot to mention) taking the dot product leads to the answer.
|
keradeek
2011-09-23 17:50:54 |
Actually, I made a mistake. The lowest energy is when angular momenta are aligned, not oppositely aligned. I should also mention that the x and y components average out to zero. Is there a way to 'modify' posts? I find it annoying that I can't modify my post
|
keradeek
2011-09-23 18:24:03 |
I need to point out that the operator (S_1 + S_2)^2 (with hats on S_1 and S_2 to signify that they are operators, not scalars) does not automatically yield the eigenvalue (S_1 + S_2)(S_1 + S_2 +1) as the solution suggests. The operator J = S_1 + S_2 (with hats on them) is the angular momenta addition operator, and J can take on a range of values from (S_1 + S_2) down to |S_1 - S_2 | in integer steps. For the ground state, the eigenfunction with J = S_1 + S_2 (scalar) will yield the lowest energy, hence the answer is D, and B.
|
keradeek
2011-09-23 18:47:08 |
J = S_1 + S_2 means of course, that they are aligned (as much as the uncertainty principle will allow). Conclusion: the ETS screwed up!
|
|  | flyboy621
2010-11-05 21:13:13 | In hindsight, I think you can arrive at a reasonable guess here without doing all that algebra.
The ground state energy should be negative, which rules out A.
It's not going to be a simple product of S1 and S2, since quantum angular momentum is never that straightforward. So B is pretty much out.
C doesn't make sense because it isn't symmetric upon interchange of S1 and S2 (the overall sign changes).
I can't rule out D.
E looks unlikely because it doesn't seem likely that you would need to divide by anything.
Pretty rough, I know, but hey--you only get a couple of minutes. |  | astro
2008-10-15 09:19:34 | If you multiply out all terms of (D), doesn't it just reduce to (B)?
medellin
2008-11-01 13:02:31 |
I agree with you!!
|
99percent
2008-11-06 08:08:27 |
Yes..!! and I marked B while solving this problem only to see that it is wrong..!!
FUCK the ETS..!!
|
Herminso
2009-08-21 15:41:36 |
That's true only if you assume that S1 and S2 commute, but it's not true in general. Then the best answer choice is (D) since the angular momentum operators S1 and S2 not necessarily commute!!
|
Herminso
2009-08-21 15:51:38 |
Now, I can see that you are really right since they use S1S2=\frac{1}{2}\left((S_1+S_2)^2 - S_1^2 - S_2^2\right), that's mean that S1 and S2 commute truly. Thus the choices are really confuse since (D) can be reduced to (B).
|
munster
2009-10-06 17:34:51 |
I made the same mistake initially, but after thinking about it a little bit, the difference between B and D is actually quite important. Particularly, we are not looking at the spin in a particular direction which has an operator 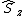 , and is well-defined. However, the total spin is only well-defined for , and is well-defined. However, the total spin is only well-defined for 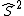 , i.e. , i.e. 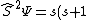\Psi) . For this reason, the energy of the ground state should not strictly be "defined" as b, but as d. ETS IS trying to trick us, but we should be wary of the fact that the Hamiltonian itself should not be defined by total spin operators that are not squared (i.e. they are asking which of the correct answers is "more correct"). . For this reason, the energy of the ground state should not strictly be "defined" as b, but as d. ETS IS trying to trick us, but we should be wary of the fact that the Hamiltonian itself should not be defined by total spin operators that are not squared (i.e. they are asking which of the correct answers is "more correct").
|
echo
2009-10-26 23:33:48 |
Scalars always commute, and 1 + 1 is equally correct as 2 as far as arithmetic is concerned. They must have messed up.
|
raymondtco
2010-11-10 16:59:39 |
I totally agree D is equivilant to B since the S's in the express are nothing but scalar quantities. Of course they commute.
|
keradeek
2011-09-22 02:18:08 |
so what is the final word on this? is D the same as B?rn
|
ewcikewqikd
2014-07-14 15:17:23 |
"This problem can be solved (without much knowledge of quantum mechanics) by noting the following general arithmetic trick: 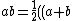^2 - a^2 - b^2)) " "
This is COMPLETELY WRONG!
^2 - a^2 - b^2) = \frac{1}{2}(ab+ba) ) , it equals , it equals 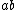 only if only if 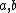 commute. In the context of the problem, commute. In the context of the problem, 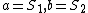 . .
So in their solution, they immediately made the assumption that 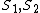 commute. commute.
This means that if "the trick" is true, 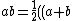^2 - a^2 - b^2) = \frac{ab+ba}{2}) , then answer B is equivalent to answer D. , then answer B is equivalent to answer D.
The solution is BS, PROVE TO ME THAT THE ANSWER IS D WITHOUT USING "THE TRICK" THEN I WILL BELIEVE IT.
|
cgrman1
2015-03-25 10:12:35 |
Instead of the "trick"
I thought of it as:
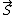 defined as ( defined as (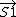 + + 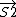 ) )
so
S^2=(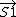 + + 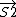 )dot ( )dot (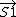 + + 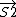 ) )
=S1^2+S2^2+2 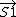 * * 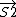
Rearranging,
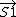 * * 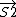 = 1/2[ = 1/2[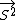 - S1^2 - S2^2] - S1^2 - S2^2]
Let S^2= S(S+1) with S= S1+S2, and plug in:
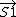 * * 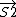 =1/2[(S1+S2)(S1+S2+1)-S1(S1+1)-S2(S2+1)] =1/2[(S1+S2)(S1+S2+1)-S1(S1+1)-S2(S2+1)]
Then you just have to multiple by -J to get your answer.
See The Heisenberg model for ground state in the ferromagnetic case for similar calculations of spin.
|
cgrman1
2015-03-25 10:16:25 |
But I did not mean to imply that it fixes the commute issue, just that instead of using the formula/trick, I did that
|
|  | scorinaldi
2007-10-18 21:03:50 | hi yosun, great site.
what is the "proper" ( i.e. traditional ) way to solve this problem?
|  | Richard
2007-09-28 13:31:11 | I believe there is a typo.
You have on the last line, \psi=(A+B)(A+B+1)\psi) . .
I believe it should be, ^2\psi=(A+B)(A+B+1)\psi) by generalization. by generalization.
|  | pablojm
2006-10-28 16:13:15 | Is it really ok to generalize A^2psi=A(A+1)psi and B^2psi=B(B+1)psi to (A+B)^2psi=(A+B)(A+B+1)psi?
Maybe I'm just confused, but it doesn't seem very obvious why that works.
tonyhong
2008-10-04 08:32:00 |
this generalization validates only if we want the ground state energy(minimum), at this time A vector + B vector = (A+B) vector, and (A+B)vector^2=(A+B)(A+B+1)
caution: this is only ground state, for other cases A vector + B vector ?= (A+B) vector
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
