|
GR9677 #33
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
wittensdog
2009-10-30 16:24:53 | I can't help but comment that I think some of the explanations here are a little bit too complicated. This is a problem that should be no more than 10 seconds, and we don't need to think about bras and kets or anything like that.
For eigenstates of some quantity, which the spherical harmonics are for angular momentum, the probability of a measurement turning up a value associated with an eigenstate is just the square of the coefficient on that state. There are two states with l = 5, so we immediately just take the sum of the squares to get the total probability; 9/38 + 4/38 = 13/38.
In my opinion, any analysis more complicated than that is too much. |  | rawr
2009-09-24 20:14:16 | An even simpler way is just to realize that since two of the three states have l=5, the probability that it is in either of those two states is the same as the probability that it is NOT in the other state. So if you find the probability of the other state (25/38) and just subtract that from 1, you get (C). |  | tau1777
2008-11-06 17:03:38 | i get the ket-bra manipulation part, but i still don't see how we take care of the fact that you're supposed to square this result. |  | cyberdeathreaper
2007-01-14 11:56:41 | Could someone expand on this calculation? I don't follow how to get it.
grae313
2007-10-31 12:37:49 |
If your wavefunction is given by 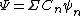 then the probability of finding the particle in the nth state is then the probability of finding the particle in the nth state is ^2) . In this case there are two quantum numbers, but you still just square the . In this case there are two quantum numbers, but you still just square the 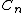 's that have the correct value of 's that have the correct value of 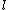 and add them together. and add them together.
|
evanb
2008-06-30 16:38:53 |
Call each spherical harmonic | l, m >.
We know, because spherical harmonics are orthonormal, that
<  , , 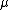 | l, m > = | l, m > = 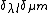
The operator we want to apply is
{ 1 if l = 5, 0 if l not = 5 }
Applying that operator to any ket | l m > yields zero if l isn't 5, and yields | 5 m > if l IS 5.
Taking <  | operator | | operator |  > gives us the following: > gives us the following:
(5 <1 1| + 3 < 5 1 | + 2 <5 -1| ) / 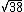 * ( 3 | 5 1> + 2 |5 -1>)/$\sqrt{38} * ( 3 | 5 1> + 2 |5 -1>)/$\sqrt{38}
Contracting, that yields, ( 3^2 <5 1| 5 1> + 2^2 <5 -1|5 -1> ) / 38
Simplifying, (9+4)/38 = 13/38, which is answer (C).
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
