|
GR9277 #91
|
|
|
Problem
|
|
\prob{91}
The particle decay 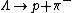 must be a weak interaction because must be a weak interaction because
- the
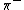 is a lepton is a lepton
- the
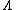 has spin zero has spin zero
- no neutrino is produced in the decay
- it does not conserve angular momentum
- it does not conserve strangeness
|
Advanced Topics }Strangeness }Strangeness
Elimination time:
(A) Only muons, neutrinos and electrons are leptons. Moreover, the pi-meson is a meson, which is a hadron with baryon number 0. (Hadrons interact with the strong nuclear force, while leptons interact with the weak nuclear force, em force, and possibly even the gravitation force.)
(B) The lambda has spin 1/2, as do most baryons. (The mesons have spin 0, but positive strangeness numbers.)
(C) Lepton number is already conserved, since none of the particles involved have non-zero lepton numbers. Thus, introducing a neutrino would violate (electron) lepton number conservation.
(D) No reason why...
(E) Only hadrons have non-zero strangeness (strangeness was proposed when strong particles interact as if weak particles---i.e., instead of having super-fast decay times characteristic of strong-force particles, their decay times appeared as if weak-force decays). Protons have 0 strangeness, as do pi-mesons, even though they are both hadrons. However, the lambda has -1 strangeness. Thus, strangeness is not conserved. |
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
enterprise
2018-03-31 21:42:59 | And mesons can have non-zero strangeness as in the Strange B meson. |  | enterprise
2018-03-31 21:39:42 | The official answer is wrong. Taus are also leptons. |  | JyxyL
2012-02-18 09:09:02 | I would just like to add, that reading sections 1.1 through 1.6 in Griffiths elementary particles text (I used the 2nd edition) tells you everything you need to know about this problem. Its about 15 pages of interesting, easy reading.
|  | ben
2006-11-01 20:23:18 | in regards to the explanation of choice (a), the tau is also a lepton (just in case that particle shows up on the test =) ) |  | kevglynn
2006-10-10 10:08:56 | Isn't there a contradiction in this solution? First I see "The mesons have spin 0, but positive strangeness numbers.)" Then I see "Protons have 0 strangeness, as do pi-mesons." Therefore, mesons have positive (non-zero I would infer) strangeness, but pi-mesons, which are mesons, have 0 strangeness. Please explain if you get the chance.
Shoshe
2006-11-03 17:43:20 |
Mesons are particles composed of one quark and one antiquark. Baryons are particles composed of three quarks. Hadrons are anything composed of quarks/antiquarks.
Pi mesons have zero strangeness -- they're composed of up and down quarks/antiquarks. Protons are composed of two up quarks and a down quarks (note that neutrons are composed of two down quarks and an up quark. The way I remember this is "a neutron is a dud" because it's neutral), so they have zero strangeness too.
Also, I'm pretty sure that strangeness is backwards -- S=-1 if the particle has a strange quark, and S=+1 if the particle has a strange antiquark.
|
|  | crichigno
2005-11-11 13:36:50 | Strangeness is a quantum number asigned to particles with an s quark content. 1 for s and -1 for anti s. Protons and Pions have no s quarks while Lambda´s have -1.
Strong forces conserve this number, but weak forces admit 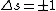 . Therefore (E) is the correct choice. . Therefore (E) is the correct choice.
yosun
2005-11-11 21:15:56 |
crichigno: thanks for the filler. just finished giving myself a crash-course in particle physics. i've posted the solution for this now.
|
student2008
2008-10-16 12:44:15 |
You're not quite right. Strangeness of particles with  -quark are -1, and antiquark 1. -quark are -1, and antiquark 1.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
