|
GR9277 #54
|
|
|
Problem
|
|
\prob{54}
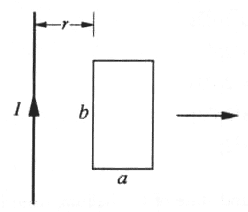
A rectangular loop of wire with dimensions shown above is coplanar with a long wire carrying current I. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated.
What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop as the loop is pulled?
Induced Current ... Force on Left Side ... Force on Right Side
- Counterclockwise ... To the left ... To the right
- Counterclockwise ... To the left ... To the left
- Counterclockwise ... To the right ... To the left
- Clockwise ... To the right ... To the left
- Clockwise ... To the left ... To the right
|
Electromagnetism }Faraday Law }Faraday Law
The induced current would act, according to Lenz Law, to oppose the change. In this case, since the field is decreasing (the wire is being pulled away from the field), the induced current would act to increase the field. On the side closest to the long wire, it would thus point in the same direction as the current from the long-wire. This eliminates all but choices (D) and (E).
Now, since the rectangular loop wire cannot induce a force on itself, the force is due to the field from the long wire. To the left of the loop, the long wire has a field pointing into the page, and thus the force there is left-wards. One can check again that choice (E) is right by right-hand-ruling the field on the right side of the loop. Since the field due to the long wire is again into the page, the force here is towards the right (since the current runs down the page on the right side of the loop).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
ETScustomer
2017-09-23 17:12:49 | Though the sign of  is obvious, ETS should have specified that is obvious, ETS should have specified that  is positive. is positive. |  | Sats
2014-10-19 22:45:48 | I disregarded Lenz's Law and just used Lorentz force:
F = q(v x B)
So since the left side is closer, the force pointing up is stronger than the force pointing up on the right side, so you see that the current is necessarily clockwise.
From there, you can similarly use the lorentz force law to say that the two closer wires attract, so the force is to the left.
Thought this was a really easy solution. Thoughts? |  | jimjam
2012-11-02 14:38:31 | Shouldn't the answer be D? Everything is correct up to the direction of the forces on left and right side. Upward current on the left side crossed with B into the page produces leftward force, but we're forgetting to multiply by a charge -q since the current is electrons. This would flip both forces.
homa
2013-10-15 13:38:29 |
You have to decide from the beginning if you are using conventional current (positive charge carriers) or "true" current (negative charge carriers). For B to be directed into the page to the right of the long wire means that you used conventional current in that wire (otherwise, B would be directed out of the page). Thus, you have to be consistent and use conventional current when considering the current through the loop. If you used true current in both the long wire and the loop, you would get the same answer (E) in the end. The key is consistency, using the same definition of current throughout the entire problem.
|
|  | checkyoself
2011-10-03 12:46:06 | -nature abhors a change in flux therefore the net current flows clockwise (the left hand side is closer to the wire and will have a larger current induced in it).
-RHR: index=B field, thumb=current, 2nd finger=force.
-since the induced currents run opposite to each other the forces that they feel due to the wire are opposite |  | mvgnzls
2011-09-15 19:31:06 | Why make it hard on yourselves people:
from knowing the current in the loop is clockwise
and knowing that
parallel currents attract and antiparallel repel
left side is parallel = attracts = left
right side is antiparallel = repels = right
thats it folks! |  | walczyk
2011-04-03 05:34:09 | I am notoriously bad with E+M, but I think I conceptually followed this problem but with some errors along the way. I still don't really understand how a clockwise current within the loop opposes the motion of the loop. The loop is being pulled away and to the right from a current-carrying wire that is flowing up. So...here is how I understand it. There is a negative change in flux through the loop because as you pull away from the wire you also pull away from its local field. We can visualize Lenz' Law by imagining the force the between two current-carrying bodies, if one is pulled away the potential between them decreases, as if an induced current in the opposite direction has reduced the voltage. Lenz' Law says that there is an induced current that counters this imaginary induced current (it is actually the change in flux density) The induced current goes AGAINST the change in flux density. Confusing yes. So imagine the dirrection of current in the loop if it was cancelled the effect of the stationary wire. It would be counter-clockwise as the closest side would move against the wire. The induced current is therefore counter-clockwise! The tricky part I found was actually what velocity you are concerned with when calculating the magnetic force. It is not the motion of the loop, or the motion of the current in the wire, but it is the motion of the current in the LOOP. F=v x B. B is into the page!! That's my two cents.
Da Broglie
2011-04-07 16:13:28 |
Walczyk, I think we should be careful here, Lenz's law states "An induced current has a direction such that the magnetic field it produces, opposes the change in the magnetic flux that induced the current." The induced current in the problem is actually clockwise and i dont think that we can use the 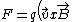) equation because we are dealing with currents and length vectors not charges and velocities. The difficulty of this problem is that of having to translate the action of a magnetic field to that of the force produced on a wire by the magnetic field. equation because we are dealing with currents and length vectors not charges and velocities. The difficulty of this problem is that of having to translate the action of a magnetic field to that of the force produced on a wire by the magnetic field.
I believe that the best way to look at this problem is to recall Griffiths' translation of lenz's law: "Nature abhors a change in flux" (page 304, Introduction to Electrodynamics, third edition). Applied to this problem we see that the magnetic flux is being decreased about the wire loop. Therefore forces will be induced to try to prevent the decrease of magnetic flux (an overall force on the wire loop to the left). Recall (1) that parallel currents in parallel wires result in an attractive force between the two wires and (2) that the force between two parallel wires is proportional to inverse of the distance between them. We see at once that choice (E) is correct since an overall force to the left is created and that the current directions are correct.
The more rigorous way to solve this problem would be to use the right hand rule to find the direction of current in the loop that would cause an increase in the magnetic flux about the loop.
Hope this helps somebody. Good luck to all on Saturday.
|
livieratos
2011-11-08 15:21:28 |
also another way to see it is, since the magnetic field is decreasing the only way to keep the flux "unchanged" is to increase the surface A which is achieved by pulling the left side further more to the left and the right side further more to the right since the horizontal sides are not affected...
|
|  | alemsalem
2010-09-27 06:57:43 | the loop could produce a force on the left and right sides (even though the total force would add up to zero)
but they are in the same direction as the force from the original current. |  | Rune
2007-10-28 15:52:10 | To determine direction, here's another way if you hate the right hand rule:
if you have two wires, with current in the same direction, they attract. If the current is in the opposite direction they repell. So if you consider the wire, and the side of the loop, they have current in the same direction, so they should attract, and therefore the force on that segment should be to the left. On the other hand, the right side has current that is going opposite of the main wire, so the wires repel, a force to the right. |  | Andresito
2006-03-27 16:04:03 | [Request]
Express in the solution that Force = I x B. Helps on recalling and does not make the solution considerably longer.
Thank you
agaliarept
2006-12-01 17:36:42 |
My thoughts exactly. Just needed a simple clarification. Thank you Andresito.
|
Kabuto Yakushi
2010-09-04 09:14:58 |
The formula for a force on a current is actually:
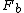 = =)
where L is the length vector of the current. But here your formula works as the length vector isn't changing.
|
|  | jax
2005-12-05 15:33:28 | I have always hated the right hand rule. I keep doing it and I'm getting the force either up or down (I know that makes no sense and I guess somehow I am doing the right hand rule wrong)
Here's what I'm doing. thumb goes in the direction of the velocity of the loop (to the right). My fingers are pointing down because the field on the right side of the long wire points down. Now apparently my palm is supposed to point in the direction of the force. My palm is facing forward which seems to be the equivalent of 'up' in the direction of the current. What am I doing wrong? Maybe I have a deformed hand. :(
At least I get the right answer if I actually compute a cross product...
jax
2005-12-05 17:44:24 |
Actually after putting some more thought into this, I still cant get the right direction of the force when doing a cross product, but I'm convinced that I am doing something wrong. I was trying to use the Lorentz force law 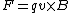 but that doesn't seem to work. but that doesn't seem to work.
I found some old undergrad notes where the prof wrote that two wires with current traveling in the same direction attracted each other (thus opposite currents repel) and that's as much explanation as I can find. Can anybody elaborate?
|
gatboja
2005-12-06 14:54:49 |
Hey jax. I'm thinking if your thumb goes in the direction of the current instead of the velocity of the loop, that should work. If you're dealing with a single moving charge, then the thumb is in the direction of the velocity (which is the dir'n of the current).
|
yosun
2005-12-06 19:25:50 |
jax: there's another right-hand rule for currents. 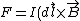 , where dl is the length element of the current. in this case, since the problem asks for the force on the loop, B is due to the long wire and dl is the length/direction of the current in the loop. , where dl is the length element of the current. in this case, since the problem asks for the force on the loop, B is due to the long wire and dl is the length/direction of the current in the loop.
|
yosun
2005-12-06 20:14:41 |
jax: the right-hand-rule basically determines which unique direction the third axis should point in. so, if you like coordinate axes better, you can use that idea in lieu of the RHR. Example: suppose you have 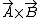 , where , where 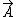 points in the x direction, points in the x direction,  points in the y direction, then the cross product points in the +z direction. (exactly as 3 coordinate axes would. however, if you have A pointing in the y direction, B in the x direction, then their cross product points in the negative z direction. etc) points in the y direction, then the cross product points in the +z direction. (exactly as 3 coordinate axes would. however, if you have A pointing in the y direction, B in the x direction, then their cross product points in the negative z direction. etc)
|
FortranMan
2008-10-01 12:12:00 |
you're probably no longer reading this site jax, but just stay with the right hand rule for a sec. Start from between the wires and move away from them.
For currents moving in the same direction, the field lines cancel in the middle, but conjoin away from the middle of the wires. For currents moving in opposite directions, the field lines conjoin in the middle, but cancel each other everywhere outside the wires.
Now think in terms of air pressure. In the former case, the lack of magnetic field on the inside compared to the outside forces the wires together, where as in the latter case the opposite happens. This is very similar to what happens with a balloon, but with air.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
