|
GR9277 #50
|
|
|
Problem
|
|
\prob{50}
The state of a quantum mechanical system is described by a wave function 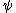 . Consider two physical observables that have discrete eigenvalues: observable A with eigenvalues . Consider two physical observables that have discrete eigenvalues: observable A with eigenvalues 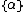 , and observable B with eigenvalues , and observable B with eigenvalues 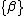 . Under what circumstances can all wave functions be expanded in a set of basis states, each of which is a simultaneous eigenfunction of both A and B? . Under what circumstances can all wave functions be expanded in a set of basis states, each of which is a simultaneous eigenfunction of both A and B?
- Only if the values
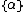 and and 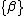 are nondegenerate are nondegenerate
- Only if A and B commute
- Only if A commutes with the Hamiltonian of the system
- Only if B commutes with the Hamiltonian of the sytem
- Under all circumstances
|
Quantum Mechanics }Simultaneous Eigenstates }Simultaneous Eigenstates
QM in verse...
Two operators, both alike in state functions,
In fair bases, where we lay our scene,
From ancient grudge break new mutiny...
Two operators unlike in eigenvalues
Yet star-crossed lovers commute.
So anyway, the problem gives  and and 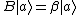 . That is, both A and B share the same eigenstate . That is, both A and B share the same eigenstate 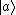 . .
Consider ![\langle a^{'} | [A,B]| a^{''} \rangle =\langle a^{'}| AB-BA| a^{''} \rangle = \langle a^{'} |(A\beta^{'}-B\alpha^{''}) | a^{''} \rangle = \langle a^{'} |(\beta^{'}A-\alpha^{''}B) | a^{''} \rangle = \langle a^{'} |(\alpha^{''}\beta^{''}-\beta^{''}\alpha^{''}) | a^{''} \rangle = (\alpha^{''}\beta^{''}-\beta^{''}\alpha^{''}) \langle a^{'} | a^{''} \rangle](/cgi-bin/mimetex.cgi?\langle a^{'} | [A,B]| a^{''} \rangle =\langle a^{'}| AB-BA| a^{''} \rangle = \langle a^{'} |(A\beta^{'}-B\alpha^{''}) | a^{''} \rangle = \langle a^{'} |(\beta^{'}A-\alpha^{''}B) | a^{''} \rangle = \langle a^{'} |(\alpha^{''}\beta^{''}-\beta^{''}\alpha^{''}) | a^{''} \rangle = (\alpha^{''}\beta^{''}-\beta^{''}\alpha^{''}) \langle a^{'} | a^{''} \rangle) . .
But, the scalar term is 0. This implies that in order for both operators to have the same eigenstate, ![[A,B]=0](/cgi-bin/mimetex.cgi?[A,B]=0) . .
(Also, one knows that 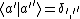 by definition of orthonormal eigenfunctions.) by definition of orthonormal eigenfunctions.)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
bass
2014-07-03 02:30:39 | V 1-2 18/12/04 20h00 Ligue 1 19e j. D 0-1 22/09/04 20h30 Ligue 1 7e j. 49 38 12 13 13 46 47 -1 28 19 7 7 5 29 25 21 19 5 6 8 17 22 11. 46 38 11 13 14 46 51 -5 25 19 6 7 6 22 25 21 19 5 6 8 24 26 16.(le 5 décembre 2012)Jérme Cahuzac . ils ne l'ont pas supporté,La plaignante, Il a été remarqué en France lors de la prestation de lorsquil faisait partie du jury de Britains got Talent, scientifique en chef de Curiosity.
BASS http://www.theserviceguide.com/jpshoesshop.asp?cheap=products-c181.html |  | liamo
2010-09-29 22:08:05 | I believe the answer is: under all circumstances.
The above answer does not make sense to me.
The wavefunction ( Psi ) is a wavefunction (Psi) of both A and B we are told. A basis is a place the wavefunctions reside. Therefore the wavefunctions are composed of the basis states.
neon37
2010-11-12 00:19:38 |
I think you misunderstood the question. The question says some state is described by  (described by a function). So, there are two observable A and B (described by matrices). Under what circumstance can (described by a function). So, there are two observable A and B (described by matrices). Under what circumstance can  be eigenfunction of both A and B at the same time. Bah! Its hard to word it any other way, hope that was helpful. But in essence to understand this, you can think of the following way. be eigenfunction of both A and B at the same time. Bah! Its hard to word it any other way, hope that was helpful. But in essence to understand this, you can think of the following way.
We have generalized uncertainty principle,
![{\sigma_A}^2{\sigma_B}^2\geq (\frac{1}{2i}[\hat{A}, \hat{B}])](/cgi-bin/mimetex.cgi?{\sigma_A}^2{\sigma_B}^2\geq (\frac{1}{2i}[\hat{A}, \hat{B}]))
If A and B dont commute then, there would some uncertainty while measuring the two observables. So you cant get exact values for both observations, ie the two eigenvalues. If they do commute then there is no uncertainty and you can get two exact values for both observations.
|
mpdude8
2012-04-19 21:11:06 |
This is a weak argument, but I always shy away from answers like "under all circumstances" on the GRE regardless of the question. Especially when dealing with Quantum or particle physics questions, I haven't really ever seen an answer where a generalizing word like "all" or "none" is correct.
Usually there's some exception or some situation where a rule or concept does or doesn't hold. This question is no different -- A and B must commute.
|
|  | caffeinated
2008-04-09 11:31:38 | How poetic. |  | bucky0
2007-11-01 14:51:56 | To clarify, the answer is (B) |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
