|
GR9277 #39
|
|
|
|
|
Alternate Solutions |
h.fei10
2012-11-04 04:20:23 | The problem is how to find a correct one from A and B.
Try this, move the origin to the right or left a little bit to make it symmetric about the V(t) axis, for example, let the new origin be 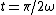 . The potenial then should be an even function. . The potenial then should be an even function.
Replace  with with 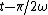 , you can turn all the sine functions into cosine functions in B, but you can't do this in A. So B is the only correct answer. , you can turn all the sine functions into cosine functions in B, but you can't do this in A. So B is the only correct answer. |  | rbot
2012-07-30 20:29:17 | My solution is simple, but lengthy when put into words. I hope it helps!
We know that both A and B satisfy the condition that ) and and ) are zero. Another condition is that for all the points between are zero. Another condition is that for all the points between 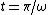 and and 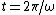 , V(t) must be -1. , V(t) must be -1.
For 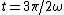 (the middle point between (the middle point between 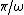 and and 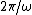 ), ),
 = -1) and and
 \omega 3\pi/2\omega ) = -1) . .
This would make it seem like both (A) and (B) are still in BUT also know that at points between 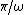 and and 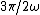 the signal is still -1. the signal is still -1.
If we try 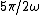 for all possible n, for all possible n,  = +1) . Clearly that is not -1. However . Clearly that is not -1. However +1) * \omega 5\pi/2\omega ) = -1) , which satisfies the signal depicted, and so on... , which satisfies the signal depicted, and so on... |  | packinski
2011-08-01 16:29:30 | Here is my solution: For 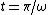 we have that we have that =0) . This, necessarily, has to be satisfied by the Fourier coefficients of as well. Answer (B) is the only one that satisfies this. . This, necessarily, has to be satisfied by the Fourier coefficients of as well. Answer (B) is the only one that satisfies this. |  | diane
2010-01-05 21:39:32 | First change the variable from x to 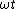 with dx = with dx = 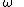 dt. Then the dt. Then the  's cancel when you do the integral. 's cancel when you do the integral.
={\Sigma}_1^{\infty} A_n sin \; n \omega t)
Use orthonormality and multiply both sides by sine and integrate:
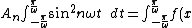sin \; n \omega t dt)
 = \frac{1}{n } [(cos n \omega t)_{-\frac{\pi}{\omega}}^0 + (-)(cos n \omega t)_0^{-\frac{\pi}{\omega}})
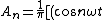_{-\frac{\pi}{\omega}}^0 + (-)(cos n \omega t)_0^{-\frac{\pi}{\omega}})
For even n, 1-1 =0. For odd n, replace n with 2n-1 or change the sum to start at zero instead of one, and replace n with 2n+1.
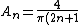}) |  | Simplicio
2009-03-27 09:46:19 | After establishing that the function is odd and left with (A) and (B), the best way to proceed is to ask:
"How do I build a square wave using sine waves?"
Consider sin(wt), it should be obvious that the period is t = 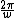 which is what we want. Next consider sin(2wt), which has a period of t= which is what we want. Next consider sin(2wt), which has a period of t=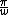 . If you add this to the first sin(wt), it adds in phase for the first half of the square (0 < t < . If you add this to the first sin(wt), it adds in phase for the first half of the square (0 < t < 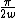 ) and anti-phase for the second half ( ) and anti-phase for the second half (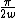 ) < t < ) < t < 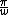 ) ), so it cannot produce a square-shape. ) ), so it cannot produce a square-shape.
If you repeat this, you find that only the odd sin(wt), sin(3wt), sin(5wt) etc ... would work hence (B) is the answer! |  | Maxwells_Demon
2008-09-21 05:29:19 | The expressions in (A) and (B) are the same (confirmed by my math, my textbooks and online)
http://mathworld.wolfram.com/FourierSeriesSquareWave.html" target="_blank">Link #1
http://www.sfu.ca/sonic-studio/handbook/Fourier_Theorem.html" target="_blank">Link #2
(A) and (B) are ultimately the same. The real answer lies in the region you are integrating. If you are integrating from -L to L, you will get the expression in (B) and if you integrate from 0 to 2L, you will get the expression in (A) (where L = pi/w in this case). Do the integration for each to see :).
Since the graph crosses the V(t)=0 axis you should integrate from -L to L and arrive at the answer (B) because that is what the graph tells you. If there was no square wave on the negative t-axis then the answer would be (A). After exhausting this problem I'm not sure how else to solve it to make it easier in a test-setting situation - but the integration does give you the correct solution integrating it from -L to L as the V(t) graph implies. |  |
|
|
Comments |
ahmedali
2017-08-30 13:35:15 | here is a valid solution but kinda lengthy. \r\nas all us thought the solution should be A, or B because they bare both odd functions.\r\nnow to choose between them, both A,and b give zero if we put t=(Pi/Omega), but here is the thing, we can take the limit as n goes to zero for Sin(2n+1)Pi/(2n+1)pi, that would give non zero, and that is the only term can satisfy this relation n=0, however we cannot do that in A because the series starts from n=1 and we do not have the n=0 term. so the answer should be B
enterprise
2018-03-31 20:18:51 |
I can\\\\\\\'t understand what you are trying to say here. My impression is that this is complete nonsense.
|
|  | kap09c
2013-10-17 16:04:48 | The featured solution makes an incorrect statement. Choice A is not trivially zero (note that omega and t can take on any values). What should be said is that for all integer multiples of pi/omega the function is zero, thus making it the incorrect choice |  | h.fei10
2012-11-04 04:20:23 | The problem is how to find a correct one from A and B.
Try this, move the origin to the right or left a little bit to make it symmetric about the V(t) axis, for example, let the new origin be 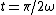 . The potenial then should be an even function. . The potenial then should be an even function.
Replace  with with 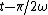 , you can turn all the sine functions into cosine functions in B, but you can't do this in A. So B is the only correct answer. , you can turn all the sine functions into cosine functions in B, but you can't do this in A. So B is the only correct answer. |  | MuckFluck
2012-10-08 13:07:32 | The square wave is antisymmetric to 0 and symmetric to pi/w, hence the harmonics should fulfill this as well. This is only the case for B. |  | rbot
2012-07-30 20:29:17 | My solution is simple, but lengthy when put into words. I hope it helps!
We know that both A and B satisfy the condition that ) and and ) are zero. Another condition is that for all the points between are zero. Another condition is that for all the points between 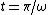 and and 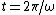 , V(t) must be -1. , V(t) must be -1.
For 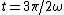 (the middle point between (the middle point between 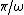 and and 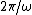 ), ),
 = -1) and and
 \omega 3\pi/2\omega ) = -1) . .
This would make it seem like both (A) and (B) are still in BUT also know that at points between 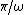 and and 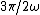 the signal is still -1. the signal is still -1.
If we try 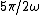 for all possible n, for all possible n,  = +1) . Clearly that is not -1. However . Clearly that is not -1. However +1) * \omega 5\pi/2\omega ) = -1) , which satisfies the signal depicted, and so on... , which satisfies the signal depicted, and so on... |  | mpdude8
2012-04-19 20:49:47 | The answer supplied by ETS is correct, 100%. I took a course solely dedicated to Fourier Analysis, and the answer is most definitely B. A and B are not the same answers -- B only takes half of the terms from 1 to infinity.
However, the assertion that sin(n*w*t) is always 0 for all n is very wrong. sin(n*w*t) is 0 for all n, if w*t happens to equal a multiple of pi.
Another commenter suggested that B was the only answer that satisfied the condition that V(t) = 0 at (pi/w), which is not true either, as the slope is infinite at that point. |  | packinski
2011-08-01 16:29:30 | Here is my solution: For 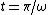 we have that we have that =0) . This, necessarily, has to be satisfied by the Fourier coefficients of as well. Answer (B) is the only one that satisfies this. . This, necessarily, has to be satisfied by the Fourier coefficients of as well. Answer (B) is the only one that satisfies this.
IvanHin
2017-05-01 04:18:12 |
it seems answer A also satisfies your test.\r\n
|
|  | packinski
2011-08-01 16:26:59 | Here is my solution: For 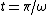 we have that we have that =0) . This, necessarily, has to be satisfied by the Fourier coefficients of . This, necessarily, has to be satisfied by the Fourier coefficients of ) as well. Answer (B) is the only one that satisfies this. as well. Answer (B) is the only one that satisfies this. |  | Crand0r
2010-11-12 19:14:07 | I like how the problem states that n ranges from 1 to 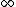 , and then the correct answer has it range from 0 to , and then the correct answer has it range from 0 to 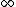 =P =P |  | Almno10
2010-11-12 15:05:57 | Try this one.
Throw out the cosines, this thing is odd. Now its A or B.
Realize that each sin wave in the series must be positive just to the left of t = pi/w. The picture shows this.
Use t = pi/w - delta, for some tiny positive delta. Then plug in n=1 in both choices. This works out, but at n=2, choice A fails. sin(2w(pi/w - delta)) = sin(2pi - delta'). That negative, so we better skip the evens! 2n+1 will do that, choose B. |  | Almno10
2010-11-12 15:05:13 | Try this one.
Throw out the cosines, this thing is odd. Now its A or B.
Realize that each sin wave in the series must be positive just to the left of t = pi/w. The picture shows this.
Use t = pi/w - delta, for some tiny positive delta. Then plug in n=1 in both choices. This works out, but at n=2, choice A fails. sin(2w(pi/w - delta)) = sin(2pi - delta'). That negative, so we better skip the evens! 2n+1 will do that, choose B. |  | antigravity
2010-11-09 08:01:28 | I had a query...
Let's have a look at the behaviour of the options at t =0.
The first two involve sines so wont they go to zero whereas V(t=0) = 1.
So we will have to throw away the first two options then?
neon37
2010-11-11 21:17:05 |
Thats not the right approach here. You should be looking at odd or even rather than value at t=0. Fourier series, unless you can actually add all the way to infinity is an approximation. So it is not necessary that exact values at all points be satisfied. It is good as long as the basic nature of the graph can be approximated.
|
Prufrock
2013-09-03 15:40:22 |
Furthermore, it is incorrect to say the V(0) = 1; this is only true in the positive limit.
|
|  | jhelps
2010-11-06 15:35:54 | I just want to say that (A) cannot be eliminated the way Yosun describes. Sin(n*pi) is zero, but the problem never said anything about (wt) being pi. Plus, (2n+1) is an integer for all integer n, so (B) would be eliminated too if one followed this logic.
I narrowed it down to (A) and (B) and took a stab from there. I'll take 15 seconds and have a 50/50 shot any day.
neon37
2010-11-11 21:33:18 |
You dont need to guess if you just realize only odd n works here. Will take you 15 more seconds but you'll surely get it right. Glass half full is also half empty.
|
|  | archard
2010-05-22 19:56:59 | The essential things to remember about Fourier series here is that functions with discontinuities tend to have Fourier series that converge no faster than 1/n, and at the points of discontinuities the fits assume the average value of the min and max of the discontinuity. So in this case the FS should be equal to 0 at t=0. That rules out all but A. |  | diane
2010-01-05 21:39:32 | First change the variable from x to 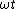 with dx = with dx = 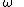 dt. Then the dt. Then the  's cancel when you do the integral. 's cancel when you do the integral.
={\Sigma}_1^{\infty} A_n sin \; n \omega t)
Use orthonormality and multiply both sides by sine and integrate:
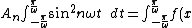sin \; n \omega t dt)
 = \frac{1}{n } [(cos n \omega t)_{-\frac{\pi}{\omega}}^0 + (-)(cos n \omega t)_0^{-\frac{\pi}{\omega}})
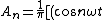_{-\frac{\pi}{\omega}}^0 + (-)(cos n \omega t)_0^{-\frac{\pi}{\omega}})
For even n, 1-1 =0. For odd n, replace n with 2n-1 or change the sum to start at zero instead of one, and replace n with 2n+1.
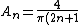}) |  | diane
2009-12-31 12:27:18 | Once you plug in the integer and evaluate n or 2n+1, the only difference between answer A and answer B is that A includes all terms and B only includes odd terms as someone else has mentioned. The reason that they actually produce the same result is that the even integers produce terms which cancel when one does the integral for the half of the period where f(x) =1 and for f(x) = -1. Those terms add to zero. Thus, while both answers produce the same result, answer A requires twice as much calculating, which makes B the best answer. Furthermore, t varies continuously, so even though it is multiplied by an integer multiple of 2pi, the argument still takes on continuous values. So, pick plus/minus values where the sine is not zero, and calculate just those two terms for n=1 and n=2 of A and you will see that the even terms add to zero. I think that on the test, that ETS wanted to see who was familiar enough with fourier series to just recognize this answer as being correct since it is a familiar first exercise in using the fourier series to approximate something. If you don't just know the answer, it requires a little time to do the integral but not much, if you know to use the orthogonality and do that. Right away the integral produces the odd terms, which are the same for both plus and minus one, adding to get answer B.
As far as this answer is concerned, it's easy to make a mistake and EVERYONE makes them. I totally love this website because it helped me so much when I first started studying to take the test. It really taught me test-taking stategies which significantly improved my score, as well as pointing me in the right direction as to where to look something up so thay I could study it more in depth. Furthermore, if you want people to be kind when you make mistakes, you should be kind to others when they make mistakes. Unfortunately, some people are still too immature to realize that they too will make mistakes, but trust me, your time will come and you will be eating your foot like everyone else. |  | phun_lover
2009-10-07 15:22:56 | Wow, there seems to be a lot of confusion on this one.rnrnFor the sake of all who might see this in the future, please allow me to attempt to clear things up.rnrnFirst, the even-odd argument eliminates C, D, E, since the cosine sums will be even but V(t) is odd.rnrnNow we know that there's a representation of V(t) in terms of a sum over sine functions only, since both A and B have this form. So write down an arbitrary sum of this form where the coefficient of the nth term is just 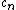 , and set it equal to V(t).rnrnNow multiply by sin(2wt) on both sides and integrate from zero to 2*pi/w. On the side with the sum, all but the second term drop out by the orthogonality of the sine functions on this interval; the only term that survives is the second, which gives a , and set it equal to V(t).rnrnNow multiply by sin(2wt) on both sides and integrate from zero to 2*pi/w. On the side with the sum, all but the second term drop out by the orthogonality of the sine functions on this interval; the only term that survives is the second, which gives a 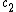 times the integral over the square of sin(2wt). Don't evaluate the integral; you know it's just some positive number.rnrnOn the side with V(t), note that over the first half of the interval, we're integrating over a complete cycle of sin(2wt); over the second half, it's an integral over a full cycle of -sin(2wt). But any integral over a full cycle of a sine function is zero (hopefully this is obvious to everyone). So this side is just zero. But that means that the other side is, too--which means times the integral over the square of sin(2wt). Don't evaluate the integral; you know it's just some positive number.rnrnOn the side with V(t), note that over the first half of the interval, we're integrating over a complete cycle of sin(2wt); over the second half, it's an integral over a full cycle of -sin(2wt). But any integral over a full cycle of a sine function is zero (hopefully this is obvious to everyone). So this side is just zero. But that means that the other side is, too--which means 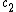 is also zero.rnrnThis now rules out choice A, since 2/pi is obviously not zero. So choice B it is. Note that we never did any explicit integration...I think that one could easily see this in less than a minute.rnrnAs an afterward, you can trivially show that all coefficients of the sin(2nwt) terms are zero by using 2n with n arbitrary instead of just 2 in the above argument. It's not really necessary here, but I thought I'd point it out.rnrnThe real key to this problem is remembering that functions of the form sin(nx) with n an integer are orthogonal on 0 <= x <= 2*pi. Otherwise, I don't see a recourse other than using some sort of heuristic argument like that given by Simplicio to guess an answer in a reasonable time frame. Of course, after you've eliminated C, D, and E, it's in your favor to guess even if you have no clue. is also zero.rnrnThis now rules out choice A, since 2/pi is obviously not zero. So choice B it is. Note that we never did any explicit integration...I think that one could easily see this in less than a minute.rnrnAs an afterward, you can trivially show that all coefficients of the sin(2nwt) terms are zero by using 2n with n arbitrary instead of just 2 in the above argument. It's not really necessary here, but I thought I'd point it out.rnrnThe real key to this problem is remembering that functions of the form sin(nx) with n an integer are orthogonal on 0 <= x <= 2*pi. Otherwise, I don't see a recourse other than using some sort of heuristic argument like that given by Simplicio to guess an answer in a reasonable time frame. Of course, after you've eliminated C, D, and E, it's in your favor to guess even if you have no clue. |  | Simplicio
2009-03-27 09:46:19 | After establishing that the function is odd and left with (A) and (B), the best way to proceed is to ask:
"How do I build a square wave using sine waves?"
Consider sin(wt), it should be obvious that the period is t = 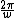 which is what we want. Next consider sin(2wt), which has a period of t= which is what we want. Next consider sin(2wt), which has a period of t=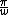 . If you add this to the first sin(wt), it adds in phase for the first half of the square (0 < t < . If you add this to the first sin(wt), it adds in phase for the first half of the square (0 < t < 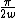 ) and anti-phase for the second half ( ) and anti-phase for the second half (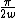 ) < t < ) < t < 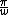 ) ), so it cannot produce a square-shape. ) ), so it cannot produce a square-shape.
If you repeat this, you find that only the odd sin(wt), sin(3wt), sin(5wt) etc ... would work hence (B) is the answer!
liliapunto
2013-07-14 20:09:34 |
This is the way to go!! =)
|
Prufrock
2013-09-12 16:00:39 |
Thank you for the excellent, lucid answer.
|
|  | vsravani
2008-10-26 10:44:25 | The answer to the question can be obtained by the use of fourier symmetry.
For even symmetry i.e f(t)=f(-t), only cos terms would be present.
For odd symmetry i.e.f(t)=-f(-t), only sine terms would be present.
For a half-wave symmetry wave, only odd values of the sinusoidal wave (sine and/or cosine) would be present. And odd values as we know are given as (2n+1).
Note: Half-wave symmetry is given as
f(t) = - f(t+T/2)
or f(t) = - f(t-T/2)
i.e except for a change of sign, each half cycle is like the adjacent half cycle.
The given wavform satisfies odd half-wave symmetry. Hence the choice is (B).
|  | Poop Loops
2008-10-12 00:27:33 | The correct answer to this one is "Skip It".
I can't imagine figuring out that I need to integrate and then integrating both equations in 2 minutes. |  | Maxwells_Demon
2008-09-21 05:29:19 | The expressions in (A) and (B) are the same (confirmed by my math, my textbooks and online)
http://mathworld.wolfram.com/FourierSeriesSquareWave.html" target="_blank">Link #1
http://www.sfu.ca/sonic-studio/handbook/Fourier_Theorem.html" target="_blank">Link #2
(A) and (B) are ultimately the same. The real answer lies in the region you are integrating. If you are integrating from -L to L, you will get the expression in (B) and if you integrate from 0 to 2L, you will get the expression in (A) (where L = pi/w in this case). Do the integration for each to see :).
Since the graph crosses the V(t)=0 axis you should integrate from -L to L and arrive at the answer (B) because that is what the graph tells you. If there was no square wave on the negative t-axis then the answer would be (A). After exhausting this problem I'm not sure how else to solve it to make it easier in a test-setting situation - but the integration does give you the correct solution integrating it from -L to L as the V(t) graph implies.
ramparts
2009-08-09 20:32:51 |
Well, they're different in that (A) admits all positive integers, and (B) admits only the odd ones.
For this one, I'd use even/odd to boil it down to two answers and when I have two choices, I make an educated guess ;)
|
Evan
2009-11-02 21:36:16 |
It's sort of tiny and hard to read, but the summation you linked from Mathworld is summed over n=1,3,5,...
|
mike
2009-11-03 19:41:50 |
The two are NOT the same.
Choice A gives both even and odd terms in the sum:
A:  = \frac{4}{\pi} * (1 sin(\omega t) + \frac{1}{2}(\sin 2 \omega t) + \frac{1}{3}( \sin 3 \omega t) + \ldots ))
whereas choice B gives only odd terms in the sum:
B:  = \frac{4}{\pi} * (1 sin(\omega t) + \frac{1}{3}( \sin 3 \omega t) + \frac{1}{5}( \sin 5 \omega t) \ldots))
Clearly the two are not the same...
|
redfish
2013-10-17 18:20:52 |
The Wolfram link you provide specifies that the sum is only over the ODD n's. Then yes, this sum is the same as B, but as written, A and B are not the same
|
|  | Maxwells_Demon
2008-09-21 03:55:49 | How are you wrong, kolahalb? |  | kolahalb
2007-11-06 03:14:43 | OK...what I said earlier was wrong...It was a careless mistake.Sorry. |  | kolahalb
2007-11-05 20:42:54 | Buddy,all of you have overlooked another possiblity.Bot the solutions (A) and (B) are correct. Because they are identical!!!
Say,m=(2n+1)
Thenm the solution(B) becomes idenetical with (A) as n=0 in (B) corresponds to m=1 if you choose the variable to be m.Now,just replace n by m and you get (A). |  | jburkart
2007-11-01 01:01:48 | Do these solutions ever get corrected? Many are good, but at least 10% are flagrantly incorrect, and some seem almost willfully specious, as with this one. welshmj is correct |  | maze
2007-10-11 06:43:29 | ric makes the correct point. Stated another way, V must be an odd function with respect to a "new origin" at pi/w. |  | Gaffer
2007-10-08 15:09:33 | Think pictures. To get the sharp down edge at pi/w you need the sine functions that have a negative slope at pi/w. The odd frequencies have this character whereas the even frequencies have a positive slope at pi/w.
Try drawing out the first, second, third harmonics.
Jeremy
2007-10-31 11:03:01 |
I too recommend quick sketches of ) for for 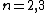 . These are the second terms from answer choices (A) and (B), respectively. ric, maze, Gaffer, and now, I, are all saying the same thing, it's just a question of what perspective you want to take. My twist is to use this criterion: the solution must be even about . These are the second terms from answer choices (A) and (B), respectively. ric, maze, Gaffer, and now, I, are all saying the same thing, it's just a question of what perspective you want to take. My twist is to use this criterion: the solution must be even about 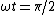 . From those quick sketches, you see that only answer choice (B) matches this criterion. . From those quick sketches, you see that only answer choice (B) matches this criterion.
|
|  | hungrychemist
2007-09-22 19:54:51 | sin(nwt) is not trivially zero for all t. therefore, the suggested solution don't work.
when t = pi/(w*2), V must equal to 1. That suggests that when t = pi/(w*2), wall the sin terms should add rather than subtract (to reach the maximum of V(t)).
sin(n*w*t) = sin(n*w*(pi/(w*2)) = sin(n * (pi/2))
but we see that if n can take even number values, above sin term will be -1, therefore choice A can be safely eliminated. |  | welshmj
2007-07-11 20:23:05 | You may eliminate A because for all EVEN n's the sine is zero so n can only be 1,3,5....that is where B comes in. the index = 2n+1 is only odd. This also explains why n goes from 0 to infinity here instead of 1 to infinity. |  | enrico
2007-01-05 11:59:20 | CONTRADICTION If sin(nwt) = 0 for all integer n, then sin((2n+1)wt)=0 , one would need to carry out the proper integrals to verify the solution. |  | enrico
2007-01-04 19:09:25 | Sr. respuesta
La funcion seno no vale cero, sino que oscila, como concluye que es cero. CRAP!!!!
Estas soluciones son una basofia. THIS SOLUTIONS ARE CRAP.
mhas035
2007-04-04 20:14:11 |
Steady Enrico, steady now.
|
|  | ric
2006-11-25 05:01:07 | the point is that =-V(t)) so we have to descard choice A so we have to descard choice A |  | grep
2006-08-31 12:53:39 | I eliminated choice A by looking at the terms in the summation. Choices A and B have identical first terms in the summation, Sin(wt) (neglecting amplitude). however their second terms are different. Choice A gives Sin(2wt) whereas choice B gives Sin(3wt). Just think about adding Sin(wt) to these two choices. Sin(3wt) makes the curve look more square-ish. Sin(2wt) just makes it look lop-sided. So choice B seems to be headed towards a square wave.
kevglynn
2006-10-02 19:56:16 |
The first terms produced by A and B are not identical. B produces sin(3wt) as its first term, not its second, since the function is as follows: sin((2n+1)wt). If it were a minus sign rather than plus, that statement would be correct.
|
mhas035
2007-04-04 20:13:11 |
The first terms are the same.
|
craklyn
2007-10-24 22:18:23 |
The first terms are different.
|
ewhite2
2007-10-27 11:57:37 |
The first terms are the same. One sum starts at 0 the other at 1.
|
|  | grep
2006-08-31 12:44:33 | |  | Mexicorn
2005-11-11 16:54:44 | I don't understand how you get rid of choice (A). If =0) for all for all  then wouldn't then wouldn't \omega t)) also be 0 for all also be 0 for all  ? ?
Almno10
2010-11-12 14:54:04 |
You actually require this. Yosun missed this part. All the sin functions in the series need to satisfy sin(nwt) = 0 when t = npi/w. (note it is not zero when t is not npi/w)
Just remember that the fourier series of just about anything skips coefficients of t (its never 1,2,3... its always 1,3,5 or 2,4,6 or 2,6 10 etc.)
|
matteoc
2012-02-07 22:15:53 |
I think we could see the thing in this way. Think about t=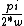 where V is not zero. In the A answer, for all the even values of n, sin will be zero. Only the odd values of n will remain. So A will become B. where V is not zero. In the A answer, for all the even values of n, sin will be zero. Only the odd values of n will remain. So A will become B.
|
|  |
|
| Post A Comment! |
You are replying to:
Wow, there seems to be a lot of confusion on this one.rnrnFor the sake of all who might see this in the future, please allow me to attempt to clear things up.rnrnFirst, the even-odd argument eliminates C, D, E, since the cosine sums will be even but V(t) is odd.rnrnNow we know that there's a representation of V(t) in terms of a sum over sine functions only, since both A and B have this form. So write down an arbitrary sum of this form where the coefficient of the nth term is just 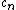 , and set it equal to V(t).rnrnNow multiply by sin(2wt) on both sides and integrate from zero to 2*pi/w. On the side with the sum, all but the second term drop out by the orthogonality of the sine functions on this interval; the only term that survives is the second, which gives a 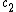 times the integral over the square of sin(2wt). Don't evaluate the integral; you know it's just some positive number.rnrnOn the side with V(t), note that over the first half of the interval, we're integrating over a complete cycle of sin(2wt); over the second half, it's an integral over a full cycle of -sin(2wt). But any integral over a full cycle of a sine function is zero (hopefully this is obvious to everyone). So this side is just zero. But that means that the other side is, too--which means 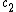 is also zero.rnrnThis now rules out choice A, since 2/pi is obviously not zero. So choice B it is. Note that we never did any explicit integration...I think that one could easily see this in less than a minute.rnrnAs an afterward, you can trivially show that all coefficients of the sin(2nwt) terms are zero by using 2n with n arbitrary instead of just 2 in the above argument. It's not really necessary here, but I thought I'd point it out.rnrnThe real key to this problem is remembering that functions of the form sin(nx) with n an integer are orthogonal on 0 <= x <= 2*pi. Otherwise, I don't see a recourse other than using some sort of heuristic argument like that given by Simplicio to guess an answer in a reasonable time frame. Of course, after you've eliminated C, D, and E, it's in your favor to guess even if you have no clue. |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
