|
GR9277 #12
|
|
|
|
|
Alternate Solutions |
Herminso
2009-09-22 19:26:52 | We have to solve the Laplace's equation in the region between the conducting plates 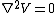 , but since the potential difference between them is independenet of the cylindrical coordinates , but since the potential difference between them is independenet of the cylindrical coordinates  and and 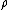 , we have then , we have then 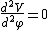 , so , so 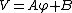 . Now by BC's . Now by BC's 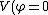=0 \to B=0) and and 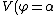=V_0=A\alpha \to V_0/\alpha=A) . Thus . Thus 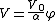 |  | mikewofsey
2006-02-10 14:55:32 | An alternative way of looking at this is that as alpha gets large, the potential goes to zero, so alpha needs to be on the bottom or the solution will blow up. Likewise, this requires that phi be on top to make sense. Of the remaining solution, chose B, because of the 1/r relationship of potential. |  |
|
|
Comments |
istezamer
2009-11-06 07:07:59 | Actually I think it is much easier to eliminate choices... If phi equals to zero the potential must be Zero.. This Keeps choices (B) and (D)..
But if Phi equals alpha, the Potential must be Vo.. So only (B) works Out !!! :D
alemsalem
2010-09-27 03:06:10 |
yup just apply the boundary conditions, and you're there
|
|  | Herminso
2009-09-22 19:26:52 | We have to solve the Laplace's equation in the region between the conducting plates 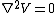 , but since the potential difference between them is independenet of the cylindrical coordinates , but since the potential difference between them is independenet of the cylindrical coordinates  and and 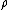 , we have then , we have then 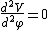 , so , so 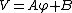 . Now by BC's . Now by BC's 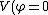=0 \to B=0) and and 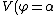=V_0=A\alpha \to V_0/\alpha=A) . Thus . Thus 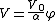
mvgnzls
2011-09-15 12:49:39 |
I dont see where you get V=A*(phi) + B
where did you get this from?
|
mvgnzls
2011-09-15 12:50:35 |
where did you get V= Aphi+B from?
|
elxcats
2011-10-31 12:01:13 |
@mvgnzls
A(psi) + B is just the solution to the differential equation. Plug it in to the equation to see.
|
RusFortunat
2015-10-22 11:01:48 |
The best solution to this problem. Short and elegant.
|
|  | bkardon
2007-09-23 13:21:19 | Another way to approach this problem is as follows:
First narrow down the choices to those that have 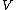 go from go from 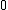 to to 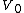 in the space between the plates (that leaves B and D). in the space between the plates (that leaves B and D).
Since there are no charges in the region between the plates, the potential must solve Poisson's equation,
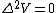
Even if you don't know what 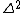 is in cylindrical coordinates, you can be confident that it includes a second derivative of \phi. Therefore, if the result of the second derivative in is in cylindrical coordinates, you can be confident that it includes a second derivative of \phi. Therefore, if the result of the second derivative in  is to be zero, there can't be any is to be zero, there can't be any 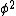 terms in the potential. terms in the potential. |  | pballjew
2006-11-26 17:49:54 | The way I found this is to note that the answer has to be zero when phi equals zero and V when phi = alpha. Then, by uniqueness, since boundary conditions are fit, you're done.
The only answer that fulfills this criteria is (B)
nyuko
2009-10-30 09:43:08 |
yes! this was what I did too! I think it is the easiest approach for this question.
|
|  | mikewofsey
2006-02-10 14:55:32 | An alternative way of looking at this is that as alpha gets large, the potential goes to zero, so alpha needs to be on the bottom or the solution will blow up. Likewise, this requires that phi be on top to make sense. Of the remaining solution, chose B, because of the 1/r relationship of potential.
hungrychemist
2007-09-19 20:27:20 |
1/r relationship of potential is not always true. Expecially when infinite (very large) charge distribution is involved.
B or D? B is correct since it's got correct units.
|
Poop Loops
2008-10-05 13:15:53 |
Also, if you only narrow it down between B, D, and A, you can see that the units only make sense for B.
|
sid
2008-10-31 04:16:37 |
dimensional analysis doesn't work in this question as all options have same unit of potential... angle in radians is already unit-less..
angle is just a number....
|
neon37
2010-11-10 10:51:39 |
Can anyone think of anytime when dimensional analysis doesnt work for angle coordinates? I cant think of any. So as heres my hypothesis. Dimensional analysis works when you have angle coordinates eventhough angles technically lack units.
|
livieratos
2011-11-08 10:55:00 |
actually i would say it's easier to think of phi since V=0 when phi=0 and only choice (B) gives that result (at least from the ones that make sense...)
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
