TimToolMan
2018-04-12 16:27:04 | We know that 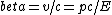 (using relativistic momentum and energy). Since (using relativistic momentum and energy). Since  we have we have 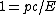 which implies which implies 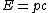 . And, from the relation . And, from the relation ^2+(mc^2)^2) , we can say that , we can say that 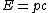 implies implies 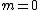 . . |  |
TimToolMan
2018-04-04 16:21:50 | Another way to think about it:\\\\r\\\\nTake ^2+(mc^2)^2) if if 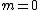 then then 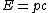 and then and then 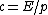 which means which means 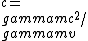 cancelling like terms gives cancelling like terms gives  when when 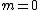
TimToolMan
2018-04-12 16:28:04 |
Disregard this one, formatting mistake. See my other comment.
|
|  |
Giubenez
2014-10-17 05:46:11 | The easiest way is surely to compare it with the photon (that is known to have a rest mass = 0).
Since

and we know that photons have finite momentum the only possible explanation is that
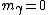
(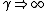 ). ).
Now our particle, having v =c must have m=0 to obtain a finite momentum.. |  |
pranav
2012-11-09 13:17:09 | One more way of doing this is by recalling the following equation:
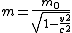
The only way anyone (including Mr. Photon) can go at  is by having a rest mass of zero. is by having a rest mass of zero.
(For those who doubt this:
The above equation can be re-written at v=c as:
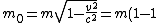=m (0)=0)
QED)
|  |
Astrophysicist
2011-10-02 11:34:45 | One can also remember that photons(which travel at the speed of light) have rest mass = 0. Thus, this particle must have a rest mass = 0 as well.
mpdude8
2012-04-19 15:15:23 |
You can't really say "particle X will automatically share the same characteristics of a photon" and deduce the answer from there, otherwise answer B also would be valid.
|
deneb
2018-10-10 04:47:41 |
The difference is that A MUST be true, so you have to pick A. Anything with v = c must be massless.
|
|  |
shak
2010-07-31 21:20:43 | Can we make a conclusion from this formula,
m=m(0)/(1-v^2/c^2)^0.5
then,
m(o)=m*(1-v^2/c^2)^0.5
when v approaches c, then m(0) goes to zero
Is this right?
thanks
neon37
2010-11-03 11:55:06 |
umm....that looks correct to me. I cant think of an arguement to counter that (atleast yet).
|
|  |
spacemanERAU
2009-10-20 08:37:41 | Also, this problem is really simple if you remember that any particle that has speed of c MUST have rest mass of zero...no math involved |  |
radicaltyro
2006-10-23 00:41:07 | It should be 
spacemanERAU
2009-10-18 18:35:28 |
agreed!
|
|  |
