|
GR9677 #86
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Particle Trajectory }Particle Trajectory
There is a force pointing upwards from the Electric field in the y-direction. Suppose the particle is initially moving upwards. Then, the magnetic field would deflect it towards the right... One can apply the Lorentz Force to solve this problem.
If the particle comes in from the left, then the magnetic force would initially deflect it downwards, while the electric force would always force it upwards. Continue applying this analysis to each diagram. It turns out that one has cycloid motion whenever the electric and magnetic fields are perpendicular.
|
|
|
Alternate Solutions |
flyboy621
2010-11-05 22:24:06 | With a B-field pointing out of the page, the particle must be turning right whenever it is moving. That leaves only (B) and (C), but (C) would be the trajectory if there were no E field. Therefore (B) must be correct. |  |
|
|
Comments |
rav
2014-09-24 11:09:58 | I'm almost certain that there is an error in the solutions. In section 5.1.2. of Griffiths EM he goes over the motion of moving charged particles in B fields.
If the direction of the velocity is only in a direction perpendicular to B, then the trajectory of the particle is a circle.
If the velocity has a component parallel to the B as well as perpendicular, then we get helical motion.
If there is an E-field and a B-field which are perpendicular to each other, then we get cycloid motion. This question addresses this case, so the answer should be the cycloid trajectory, E.
amber
2014-10-21 16:18:57 |
I agree. The answer is E
The particle is initially at rest, so no magnetic force acts on the particle. The electric force acts on the particle first and then the magnetic field can act on the moving particle.
|
amber
2014-10-21 16:25:04 |
oh wait never mind. I didn't read the question correctly
|
dc771957
2016-10-24 22:53:42 |
If the particle were initially at the origin, or somewhere else along the x-axis, at rest, it would follow motion similar to E only it would be bouncing along the x-axis, not the y-axis. Initially v=0 so the force due to the magnetic field is zero, as the particle begins to accelerate in the +y direction due to the force from the electric field, it begins to feel a force from the magnetic field, which will initially make the particle accelerate in the +x direction. For this setup, the magnetic force will always be trying to force the particle to make a right turn. As the particle begins to move in the +x direction, the magnetic field will start to pull the particle in the -y direction, keep in mind that the electric field is still acting in the +y direction. As the particle begins to return to the x-axis, with a velocity in the -y direction, following a similar path shape from answer E, it will slow down because the electric field is pulling it upwards. The particle will have enough kinetic energy to resist the pull of the electric field until it returns to the x-axis, where it will briefly stop, before repeating this process. \r\nIf you take a look at answer E, you will see that the magnetic and electric fields will be pulling the particle in the +y direction when it intersects with the y-axis; the electric field always acts in +y, and the particle will have a velocity in the -x direction with magnetic field still in the +z direction. So, no, E is not the correct answer, but that didnt stop me from picking when I first looked at this problem.
|
|  | superderec
2010-11-27 12:08:33 | it's best to suppose that the particle is fired in the x-y plane as a projectile (at an angle with the x-axis and with a low velocity) towards the x-axis .As mentioned it is moving only in the x-y plane. Since the E-field is in the +y direction, the particle will be repelled by the positively charged plate near the axis producing the E-field. so it never reaches the x-axis. (there is a minimum x) and the particle is being pushed by the B-field to perform some circular motion. Only possible answer is B. (The concept of left and right and upwards in Yosun's answer does not make sense) |  | flyboy621
2010-11-05 22:24:06 | With a B-field pointing out of the page, the particle must be turning right whenever it is moving. That leaves only (B) and (C), but (C) would be the trajectory if there were no E field. Therefore (B) must be correct.
Mr.Saul
2017-10-15 11:53:29 |
I think that you mean turning clockwise, which excludes (D). \r\nThis is a good observation.
|
Mr.Saul
2017-10-15 11:54:57 |
A Typo: \"which excludes (E)\"
|
|  | his dudeness
2010-07-30 07:15:50 | I found it easiest to just draw a diagram of the forces felt by the particle. The E-field always causes a force in the+y direction. When the particle starts moving in the +y direction, the B-field causes a force in the +x. When it is moving in the +x direction, the B-field causes a force in the -y, etc. Qualitatively, the motion of the particle is thus described by (B). |  | gt2009
2009-05-27 01:34:28 | The correct answer (B) is a helix. Cycloid motion would be (E), which is wrong.
claire
2009-10-09 14:21:19 |
Both B and E are cycloid, e is just a special case.
The problem states "a positively charged particle is moving in the xy-plane." The motion is in the xy plane, and thus cannot be a helix (which requires motion in all 3 directions)
|
nimesh.nic
2011-11-01 06:34:07 |
exectaly that's what I thought .......
|
|  | PhyAnnie
2008-11-04 06:07:49 | I was wondering... since the particle is always under the constant electric force of E*q upward, why the answer B doesn't show a upward trend, instead of being horizontal. That's strange.
f4hy
2009-04-03 19:13:19 |
It does seem strange, but it is the behavior when B and E are perpendicular. I don't remember which book but one makes this exact point when talking about cyclotrons.
|
WallStreet
2014-09-07 20:00:08 |
think about this, the B field gives a force of 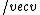 x x 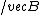 . .
If a positive charge is moving to the right, the B field gives a force in the -y direction proportional to the velocity. So a particle moving at just the right velocity would show no upward drift (the force from the magnetic field would counter the force from the electric field.
But this only occurs for a special velocity, if the velocity is different, we will end up with different motion.
|
|  | greed
2008-10-15 11:28:00 | Doesn't the cycloid motion correspond to a drift velocity that is proportional to 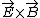 ? This would make the drift in the x direction, but choice D shows a drift in y. little confused ... ? This would make the drift in the x direction, but choice D shows a drift in y. little confused ...
greed
2008-10-15 11:30:34 |
oops, never mind: just checked the answers
|
|  | cordercom
2008-10-05 17:58:59 | I think we can use the Poynting vector in this case. The net flux of energy density and hence the net trajectory of the particle must be in the direction of E cross B= (y X z)=x. So, the net displacement of the particle must be toward the right. Answer (B) seems most appropriate.
See Griffiths, Intro to Electrodynamics 3rd Edition, pg 206 & 347
physicsisgod
2008-10-30 16:34:35 |
The Poynting vector describes the direction of energy propogation for the EM field. It says nothing about the energy of particles moving in the EM field. This is a lucky coincidence.
|
|  | buddy.epson
2006-10-14 14:27:13 | the +z direction is determined by the cross product of +x and +y (aka the right-hand-rule). |  | andreas
2005-11-10 05:00:51 | And for those who, like me, are confused by conventions, the magnetic field in the +z direction means it comes out of the page.
(I'm used to defining +z to be away from the observer, i.e. into the page)
shafatmubin
2009-11-05 14:13:55 |
Use cross product: i x j = k
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
