|
GR9677 #81
|
|
|
|
|
Alternate Solutions |
ramparts
2009-10-01 12:43:38 | Limits, limits, limits! No need to know about beat frequencies and all that fancy *physics* stuff to get this right (I didn't! :P). Just play the GRE game. One can figure pretty easily that if the string tensions are the same, the amplitude stays at 1, because then they're the same string and there's absolutely no reason for the wave to change. That eliminates D and E. Meanwhile, if the right side is EXTREMELY heavy, you expect the amplitude to be pretty darn small - so as 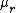 goes to goes to  , the amplitude should go to zero. This eliminates A and C, leaving only B. There you go :) , the amplitude should go to zero. This eliminates A and C, leaving only B. There you go :) |  | jmason86
2009-09-22 19:30:44 | Basically the same solution but using some test taking strategy:
ETS gave two answers with Harmonic = 6. The correct answer is PROBABLY one of these (since all the others are different). Eliminate (C) (D) and (E).
73*6 = 438. 440-438=2 but since the actual frequency is just over 73, the difference should be less than 2. Eliminate (A)... (B) remains. |  |
|
|
Comments |
calvin_physics
2014-03-27 14:24:00 | Why does it ask "number" of beats?
Why not say what is the beat frequency?
number - seems integer to me. |  | ramparts
2009-10-01 12:43:38 | Limits, limits, limits! No need to know about beat frequencies and all that fancy *physics* stuff to get this right (I didn't! :P). Just play the GRE game. One can figure pretty easily that if the string tensions are the same, the amplitude stays at 1, because then they're the same string and there's absolutely no reason for the wave to change. That eliminates D and E. Meanwhile, if the right side is EXTREMELY heavy, you expect the amplitude to be pretty darn small - so as 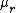 goes to goes to  , the amplitude should go to zero. This eliminates A and C, leaving only B. There you go :) , the amplitude should go to zero. This eliminates A and C, leaving only B. There you go :)
ramparts
2009-10-01 12:44:32 |
Ugh! Delete this. I was looking at problem 80. I was wondering why all the solutions talked about beat frequencies ;)
|
memorial
2010-07-08 08:19:18 |
wrong problem, buddy. we're on #81, not #80.
|
|  | jmason86
2009-09-22 19:30:44 | Basically the same solution but using some test taking strategy:
ETS gave two answers with Harmonic = 6. The correct answer is PROBABLY one of these (since all the others are different). Eliminate (C) (D) and (E).
73*6 = 438. 440-438=2 but since the actual frequency is just over 73, the difference should be less than 2. Eliminate (A)... (B) remains.
shak
2010-08-19 07:02:42 |
Can u please explain me, why are u dividing frequency of A4 to the frequency of D2 to find harmonics?
even , if then answer is close to 6 , but it is smaller than 6, and therefore answer should be 5,i.e lowest? thank you
|
alemsalem
2010-09-15 03:23:42 |
what matters is the difference not who is bigger, if you use the fifth harmonic the difference would be bigger, therefore more beats per second, the two waves add to give (approximately): rnsin(w1t)+sin(w2t) = sin(wt)*cos( w1-w2)/2 trnhere w is (w1+w2)/2 since they're almost equal you can take it to be anyone of them, |w2-w1| is the beat (angular) frequency, you're required to minimize the absolute value (cosine is even)
|
flyboy621
2010-11-05 21:25:05 |
The nth harmonic of D2 is D2*n. You can quickly estimate 440/73 is closer to 6 than any of the other answers, so the 6th harmonic would minimize the beat frequency. Then multiply 73.4 by 6 to get 440.4, which would be .4 Hz, very close to .5.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
