|
GR9677 #74
|
|
|
|
|
Alternate Solutions |
asdfman
2009-11-05 00:11:38 | Used POE.
Expect there to be a change in entropy - E is out.
Know the typical integral to find S will involve a 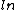 - A is out. - A is out.
Expect the entropy to increase for the system - D is out.
Based on the numbers, expect there to be a ratio as an argument of the 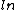 - C is tentatively out. - C is tentatively out.
I'd come back to it if there was time and run the math to see if B is actually correct. If not this logic narrows it down to 2 choices. |  |
|
|
Comments |
q
2019-10-15 15:39:09 | Cependant, Hernandez ne re?oit pas suffisamment l\'occasion de montrer ses compétences comme il joue derrière Ronaldo, Gareth Bale, Karim Benzema et James Rodriguez.\r\nq http://www.alaubergededaon.com/fr2.asp |  | q
2019-10-09 14:08:02 | Sevilla: 12-2-4, 39 pointsFollow Damon Salvadore sur TwitterFOR PLUS NOUVELLES ET MISES à JOUR SPORTS, cliquez sur ce lien pour visiter LATIN POST.\r\nq http://www.eurotrends.it/en6.asp |  | physicsphysics
2011-10-11 08:21:33 | I think this problem is a little bit tricky. To obtain the equation form of integral, the system should be changed reversibly. If this system is irreversible, the entropy change of this system is -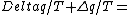 zero. zero.
physicsphysics
2011-10-11 08:24:13 |
Sorry. I confused two cases. Just reversible case is zero. irreversible case is S>=0.
|
|  | mrTrig
2010-11-05 13:50:32 | yosun, you can reduce the logarithms much faster by simply knowing that addition of two results in multiplication of arguments. } +\ln{3}) = mc\ln{(\frac{9}{5})}) |  | asdfman
2009-11-05 00:11:38 | Used POE.
Expect there to be a change in entropy - E is out.
Know the typical integral to find S will involve a 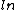 - A is out. - A is out.
Expect the entropy to increase for the system - D is out.
Based on the numbers, expect there to be a ratio as an argument of the 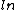 - C is tentatively out. - C is tentatively out.
I'd come back to it if there was time and run the math to see if B is actually correct. If not this logic narrows it down to 2 choices. |  | dstahlke
2009-10-09 10:53:51 | But isn't it true that 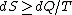 with equality only in the case where the process is reversible? This process doesn't seem reversible to me. with equality only in the case where the process is reversible? This process doesn't seem reversible to me.
kroner
2009-10-11 20:16:00 |
In the context of the whole system it's not a reversible process. From that perspective dQ = 0 so you are correct that dS > dQ/T = 0. Clearly the change in entropy is positive.
But considering the two objects separately, they're each undergoing a reversible process (being uniformly heated or cooled). The change in entropy for each can be found by setting dS = dQ/T where dQ is the heat flowing into that object. Then you sum the changes contributed by each object.
|
|  | vinograd19
2007-02-02 10:27:17 | I think there is a mistake in solution. One integral is positive, the other is negative. But in solution they are both positive.
hungrychemist
2007-10-07 21:34:32 |
Solution is correct. The sign of integral is determined solely from the limits of integration. Notice ln(3/5) itself is a minus number as expected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
