tdl17
2019-01-05 22:45:55 | You can also use dimensional analysis. Whatever that goes into the arc tangent should be purely numerical without any units, and the only answer where this happens is choice A. Vq cancels with mv^2 because they both have units of Joule. L cancels with d because they both have units of length. |  |
deneb
2018-10-08 04:12:51 | You have to divide both sides by 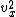 , and since , and since  is just the original velocity given in the problem, that\\\\\\\'s how you get is just the original velocity given in the problem, that\\\\\\\'s how you get 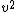 in the denominator in the denominator |  |
allenabishek
2017-08-03 19:29:24 | Why is it that in the solution to find dy, the first term is ignored ?? the kinematic equation is actually y = v0t + 0.5at^2. why is the first term ignored? |  |
dipanshugupta
2017-03-22 14:15:07 | Well A looked more beautiful. |  |
hooverbm
2012-11-02 09:15:49 | Found a super fast way of doing this.
The charge is obviously acted upon by a force due to the electric field.
For parallel plates, the acceleration due to this force only acts along the y-direction. We know:
F = qE (V = Ed ---> E = V/d)
ma = qV/d
a = qV/md
The angle of deflection should be proportional to this term, leaving only answer A |  |
soloeclipse
2010-11-04 16:31:02 | All of the answers are dimensionless.
SonOfHam
2010-11-12 22:21:52 |
+1
|
kevintah
2015-10-12 19:03:36 |
lol, this sucks!
|
|  |
shjung84
2010-10-14 21:55:12 | See dimension
The only possible choice is A of which argument indicates no dimension. |  |
Moush
2010-09-15 18:11:51 | For a completely unphysical approach, see below. To actually learn something, see other posts.
I got this via simple guessing strategy.
(L/d) shows up in 3 answers; ^2) and and ^{1/2}) only once, eliminating C and E. only once, eliminating C and E.
Vq shows up twice in the remaining answers; 2Vq once, eliminating D.
^2) just looks wrong, eliminating B. just looks wrong, eliminating B.
ryanmes
2018-10-24 01:19:02 |
I did the same thing... it works
|
|  |
dstahlke
2009-10-09 10:57:43 | The diagram threw me off here... The deflection of the final velocity is ) but the dotted lines on the diagram form a triangle suggesting they want but the dotted lines on the diagram form a triangle suggesting they want ) which I think would be equal to which I think would be equal to ) . That wasn't one of the options so in this case I suppose guessing the nearest answer would work. . That wasn't one of the options so in this case I suppose guessing the nearest answer would work. |  |
haro
2007-04-13 04:25:01 | It is simplier to think of tan = = 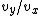
Jeremy
2007-10-15 12:01:19 |
I agree. From 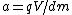 use use 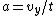 , ,  , and finally, the equation you gave: , and finally, the equation you gave: 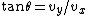 . .
|
walczyk
2011-04-05 13:27:12 |
this works well except i don't see where the  comes in? comes in?
|
|  |
yosun
2005-11-09 14:42:33 | tachyon: thanks for the typo-alert; it has been corrected. |  |
tachyon
2005-11-09 13:36:53 | typo-the correct answers is A |  |
