|
GR9677 #70
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
hanin
2009-09-29 22:49:26 | Echoing: what if you don't remember Larmor formula?
And, is there any simpler/more practical way to tackle this problem...
fjornada
2009-10-19 13:38:53 |
if you convince yourself that P can only depend on "a" and "q", here is a trick: the acceleration is actually a vector, but the power cannot depend on the direction/sign. The also power does not change if we replace "q" by "-q".
Now, you'll only have two options, either "a" and "q" appear as |a| and |q|, or as a^2 and q^2. Since EM equations usually do not have modulus sign (squaring is a more "complex" operation to be obtained from first principles), it is *reasonable* to think that P should depend on a^2 q^2.
a^4 and q^4 could work, but no answer fits.
Hope that helps a bit...
|
|  | Mexicana
2007-10-03 22:08:27 | What happens if you don't remember the Larmor formular?!?!
tareq
2007-10-06 12:58:26 |
You have to do the following:
from the concepts of electrodynamics, you know that the power radiated will depepend on q and the acceleration (a) and not on mass and velocity. A simple dimensional analysis tells you that the charge should appear raised to power two in the formula. Now the acceleration has to be raised to some power also either 1, 2, 3, 4, ... You are left only with choices (A) and (D) corresponding to powers 1 and 2.
|
Jeremy
2007-10-15 13:04:32 |
It's not clear to me how/which "concepts of electrodynamics" help in picking the parameters found in the power formula. It would be great to see a more detailed explanation there.
I also struggle to see simplicity in the dimensional analysis argument. Power has units 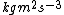 , or , or 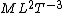 , where M, L, T, and later C stand for mass, length, time, and charge. Assuming , where M, L, T, and later C stand for mass, length, time, and charge. Assuming 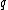 (units (units 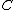 ) and ) and  (units (units  ) are the only relevant parameters in ) are the only relevant parameters in 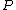 , it becomes clear that you also have to consider constants - let's assume these are , it becomes clear that you also have to consider constants - let's assume these are 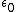 and and 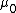 . These constants have units . These constants have units 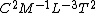 and and 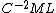 , respectively. At this point, I don't see how you can jump to an answer like " , respectively. At this point, I don't see how you can jump to an answer like "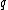 is squared" without considering the exponents adorning the other quantities of interest. I don't use dimensional analysis enough to feel comfortable continuing with guess and check, instead I use equations. In an equation, here is what has been assumed: is squared" without considering the exponents adorning the other quantities of interest. I don't use dimensional analysis enough to feel comfortable continuing with guess and check, instead I use equations. In an equation, here is what has been assumed: 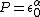 . .
|
Jeremy
2007-10-15 13:18:24 |
Oops! Clicked post, not preview...
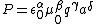 . .
By equating the units on both sides, we collect a set of equations:
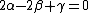 , ,
 , ,
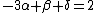 , ,
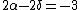 ; ;
from which we find: 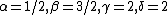 . This is correct, but it takes way too long to be a practical method to solve the problem. Does someone see an easier/faster way to implement dimensional analysis here? . This is correct, but it takes way too long to be a practical method to solve the problem. Does someone see an easier/faster way to implement dimensional analysis here?
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
