GREPhysics.NET: GR9677 #64

GR9677 #64

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Advanced Topics $\Rightarrow$ }Nuclear Physics

In symmetric fission, the change in kinetic energy is just the change in binding energy. The change in binding energy for a $N-nucleon$ heavy nucleus is the difference in energy between the initial un-fissioned heavy nucleus and the final 2 medium-sized nuclei,

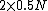$\Delta E = 2\times 0.5 N \times 8MeV/nucleon - N \times 7MeV/nucleon = N \times 1MeV/nucleon$ .

For a heavy nucleus, one has $N\approx 200$ , and thus one arrives at choice (C).
(This is due to David Schaich.)

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

petr1243 2008-02-16 21:28:31	Q=(# of nucleons)(\|change in energy per nucleon\|)rnrnUsing the mass number of a heavy nucleon(A=200)rnrnQ = (200)(8-7)Mev = 200Mev Reply to this comment
relain 2007-10-31 10:19:08	also it might help to remember that iron is the most stable nucleus with A ~ 50 and then uranium is about 250 (232, 252 whatever) so then if this is a large unstable nucleus, and each nucleon gves 1mev you're gonna get about 200... Reply to this comment
Void 2005-11-10 06:49:25	I've seen this number (200 MeV/fission) appear in a lot of elementary physics books and even a lot of lectures. If you forget everything else, just remember 200 MeV per fission... Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

1GHz Smartphone for 1 cent - best deal on a Samsung Galaxy Phone

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone