|
GR9677 #53
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
whereami
2018-04-06 01:23:24 | i think the answers are all wrong, or maybe I am making a mistake. \r\nThe problem states that orbital angular momentum is zero. That\'s not even spin. And everybody is saying that spin is zero. This really bugs me. \r\nI don\'t think L has anything to do with S. \r\nCan somebody help me ?
kronotsky
2018-10-22 03:12:24 |
Spin is indeed not conserved by itself; this is something neglected by previous answers. Total angular momentum is conserved - but in the zero momentum frame centered around the center of mass, the orbital angular momentum of emitted photons should be zero since r is parallel to p, so orbital angular momentum will be conserved and therefore so will spin. Since L and p do not commute, the resulting combined photon state must be in the kernel of the commutator (i\'m a little worried about this being true, but I really don\'t want to find out lol), which need not be true in general, so the fact that we are thinking about the center of momentum/mass-centered frame is important (i.e. this logic is more difficult to apply for less simple complicated positronium diagrams).
|
kronotsky
2018-10-23 02:14:26 |
After thinking about this a little more, if the initial angular momentum is zero, then in the COM frame both the angular momentum and the total momentum is zero for the final multiple-photon state, so L and p do commute in this special case.
|
kronotsky
2018-10-23 02:16:13 |
Also, I meant to say that \"total angular momentum is conserved and therefore so is spin\" since j = l + s and l = 0.
|
|  | gman
2010-11-10 17:51:00 | There are two kinds of positronium: ORTHOpositronium and PARApositronium. The difference is in the way the positron and electron spins align.
Ortho is the spin triplet -> total spin=1
Para is the spin singlet -> total spin=0
Since para is unchanged under charge conjugation (due to antisymmetry of fermion wavefunctions in the singlet), and since photons are negative under charge conjugation, para must decay into an even number of photons. Zero is forbidden due to energy conservation, so it's 2, 4, 6, ... Successively higher numbers of photons are less likely because of the additional vertex factors. So to lowest order, para goes to 2 photons.
Ortho on the other hand is negative under charge conjugation, so it must go to an odd number of photons. 1 is out due to momentum conservation, so thats 3 5 7, etc... again decreasing in probability.
But that's technical... Just remember this. PARA is the singlet, spin 0. zero is small, so that's a small number of photons. You need TWO lines to be PARAllel. If you have two ORTHOgonal lines, cross them to get THREE mutually ORTHOgonal lines.
I know, it's dumb. But you'll remember it on the test....
mvgnzls
2011-09-18 13:08:46 |
actually there are 3 types of positronium
the third is Di-positronium
|
|  | pkamal
2010-10-02 18:32:53 | If emission of 2 photons conserve spin, whats wrong with emission of 4 photons? It will also conserve spin.
flyboy621
2010-10-24 17:20:26 |
I think you can assume that emission of 4 photons COULD occur, but is less likely.
|
|  | South92
2009-10-20 08:18:11 | So what happens if the positronium is in the 2s state (which has zero orbital angular momentum)? My understanding is that the positronium could decay into its ground state, emitting a single photon (there would be recoil, thus conserving momentum), and anihilate to produce two more photons. Is this incorrect?
The_Duck
2010-07-05 14:39:54 |
I don't really know what I'm talking about here, but I think if you're in the singlet 2s state you can't drop down to the singlet 1s state by emitting a single photon, because of this very reason: both states have J=L=M=0, so you can't conserve angular momentum if you emit a single photon.
|
tmraotmh
2011-04-07 19:50:19 |
A photon is massless, so can't have no momentum. Thus in the center of mass frame, we can't have just one photon or momentum will not be conserved.
|
|  | WoolfianOperator
2009-10-18 18:05:16 | Here's a go.
We know that energy has to be conserved. A is out. We know momentum must be conserved, a single photon cannot have 0 momentum. B is out. We know from Feynman diagrams that a process will occur with probability 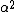 , with each vertex of the diagram contributing a factor of , with each vertex of the diagram contributing a factor of 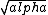 . Because . Because  equals equals  , the diagram with the least amount of vertices is most likely to occur. See Griffiths Introduction to Particle Physics for more on this. The more photons the more complicated the diagram and therefore there will be more vertices. So choice C is best of the remain 3 options. , the diagram with the least amount of vertices is most likely to occur. See Griffiths Introduction to Particle Physics for more on this. The more photons the more complicated the diagram and therefore there will be more vertices. So choice C is best of the remain 3 options. |  | phys2718
2008-10-12 08:42:45 | The comments on antiparticles are incorrect. The photon and antiphoton both carry spin 1, just as the electron and positron both carry spin 1/2 (not -1/2 for the positron). Spin is not a so-called "additive" quantum number in the sense that we simply add charge or baryon number as scalars, and in fact antiparticles carry the same spin as their particles. Two positive spins may be combined so as to produce 0 total spin (the singlet configuration) which is the case here for the positronium as well as the two emitted photons.
physicsisgod
2008-10-29 21:44:15 |
Maybe we are confusing the magnitude of a particle's spin, which is positive, and its direction, which can be up or down. Spin is a vector, really, so it's not "positive" or "negative".
|
|  | backyard
2006-11-01 23:13:38 | why not zero photons?
barefoot0
2006-11-02 19:30:21 |
Good question...
I do not think you could have a decay without emiting some kind of radiation.
I would love to hear a better answer.
|
ben
2006-11-03 14:21:57 |
can't have zero photons because of conservation of energy. since positronium is unstable the electron will soon spiral into the positron and the two particles will annihilate, producing photons. i can't think of any other particle an electron and its antiparticle could decay to.
|
scottopoly
2006-11-03 19:32:10 |
It has to emit something, just to conserve energy. 2 photons are certainly the most likely. Anything else would probably take more energy. 1 photon is forbidden by both momentum conservation and angular momentum conservation.
|
wittensdog
2009-11-03 19:58:07 |
Aside from issues involving parity conservation in EM processes and so forth, the more photons you add, the more interaction vertices you add, and you bring along another factor of alpha. So even if 3 and 4 photons were allowed, they're going to be less likely.
|
wittensdog
2009-11-03 20:33:33 |
I mean, if you want to get really anal about it and consider other forces and interactions,
1.) electrons and positrons don't feel the strong force, so rule that out
2.) forget anything to do with gravitons and quantum gravity, those decays, if they even exist, are going to be so ridiculously suppressed it's not even funny
3.) Weak interactions are also very suppressed, and really the only neutral end product of interest is a Z boson, which is much too heavy and would need to decay in a very small time to something lighter, and the cross section to go to something like a neutrino anti-neutrino pair is going to be really low, and may even violate some conservation law I'm not thinking of right now
So really the EM interaction is what we have to work with, so we're going to be working with some non-zero number of photons, since in order to conserve energy, zero photons would mean some other force is at play, since there are no particles involved in the EM interaction that are lighter than electrons and positrons. 1 photon violates momentum conservation and also I believe parity conservation, but 2 is okay. Anymore photons is going to be suppressed in the diagrams.
|
|  | comorado
2006-10-30 02:06:52 | We have conseravtion of momentum here, before the decay  , after decay must be , after decay must be 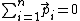 , so the most simple answer is two fotons with opposite momentum. , so the most simple answer is two fotons with opposite momentum.
barefoot0
2006-11-02 19:35:30 |
I dont think anything is said reguarding the momentum only angular momentum.
|
scottopoly
2006-11-03 19:28:45 |
You could always transform to the rest frame of the positronium, so WLOG, we know it's momentum is zero.
|
scottopoly
2006-11-03 19:29:29 |
You could always transform to the rest frame of the positronium, so WLOG, we know it's momentum is zero.
|
scottopoly
2006-11-03 19:29:39 |
You could always transform to the rest frame of the positronium, so WLOG, we know it's momentum is zero.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
