|
GR9677 #51
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Infinite Well }Infinite Well
The even wave functions always have nodes in the middle, and thus the probability density for states of even n vanish. (One can deduce this by fitting curves inside a box. The first state has no nodes in the middle, but a node at each end of the well. The second state has one node in the middle. The third state has two nodes, neither of which are in the middle. The fourth state has three nodes, one of which is in the middle.)
|
|
|
Alternate Solutions |
Richard
2007-09-27 14:34:44 | Recall the form of wave functions in an infinte well:
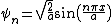)
(which if not exactly correct is close enough!)
At the center of the well, 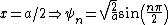)
So when  is even we get a node ( is even we get a node ( ). ). |  |
|
|
Comments |
Yurlungur
2012-03-30 21:04:24 | An alternative way to think about this problem:
Spherical harmonics 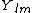 always have the following properties: always have the following properties:
1) The highest power of ) or or ) is always is always 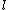
2) There is always a factor of 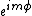 . .
We can convert ) into into 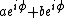 , where , where  and and 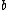 are complex constants. We can then see that we're looking at a spherical harmonic with are complex constants. We can then see that we're looking at a spherical harmonic with  and and 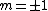 . .
Yurlungur
2012-03-30 21:07:04 |
Oops! Meant to describe problem 52 here! Sorry, if anyone is still moderating, please delete this.
|
|  | mangree
2008-10-30 07:28:45 | Typo:
The ODD wave functions always have nodes in the middle, and thus the probability density for states of even n vanish
claire
2009-09-30 11:15:27 |
Just to clarify.
In the square well energies go like n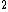 . .
For the ground state n=1. The ground state is an even function (no node in center). So the even functions in the square well potential correspond to odd n.
We want the odd functions (where theres a node in the center), and that corresponds to even n (consider n=2).
This can be a little confusing because it is the opposite for the simple harmonic oscillator. There, E~(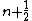 ) so the ground state corresponds to n=0, and even wave functions correspond to even values of n. ) so the ground state corresponds to n=0, and even wave functions correspond to even values of n.
Its simple once you think about it, but i just thought id compare the two explicitly
|
hybridusmanus
2010-08-16 15:33:08 |
claire is right, the n=3 state for the potential well is an even state, though 3 is odd. (Think the first state (n=1) has to be the ground state)
Use this mnemonic: For the Quantum Harmonic Oscillator, the value of n in is HARMONY with the state (1 is odd and is an odd state, 2 is even and is an even state, etc...)
|
flyboy621
2010-10-24 17:01:39 |
no typo: a node is where the wavefunction vanishes.
|
camcam
2019-09-12 15:46:59 |
I think there\\\\\\\'s a bit of confusion here between states of even n (like the question states) and even functions (where the prob. density is symmetric around the center of the well).
|
|  | Richard
2007-09-27 14:34:44 | Recall the form of wave functions in an infinte well:
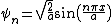)
(which if not exactly correct is close enough!)
At the center of the well, 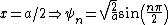)
So when  is even we get a node ( is even we get a node ( ). ).
zeper
2012-08-26 12:35:08 |
Nice way to think!! thanks...
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
