|
GR9677 #45
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-09-24 06:06:16 | I must say, what a problem. Orlando Towing Partners - I-Drive |  | flyboy621
2010-10-24 16:07:24 | We can solve this without knowing anything about AC circuits.
First, you can eliminate the circuits with diodes, since neither would behave differently at different AC frequencies (why would they?). That rules out (B) and (C).
To narrow it down further, analyze the low-frequency limit, by assuming DC voltage (lowest frequency you can get, right?). We are given that 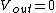 at low frequency. at low frequency.
(A) wouldn't work because the voltage across the capacitor, the resistor, and 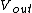 must each equal must each equal 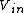 . .
(D) wouldn't work for a similar reason.
(E) is the only choice left. It looks like it would work because the capacitor would charge until the voltage drop across it equals 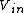 , and then there would be no more voltage drop across the rest of the circuit. , and then there would be no more voltage drop across the rest of the circuit.
We don't need to know the high-frequency behavior of any of these to know that (E) is right. |  | Blake7
2007-09-23 05:50:32 | Folks, whenever you see the symbol for a cap, two parallel, UNCONNECTED lines, you should immediately think "DC 'Block'"; a "short". And, conversely, with a cap being a DC block, it is also an AC, Hi Freq "Pass". Go back and study Max's eqns for caps if you don't get this, yet.
So, by inspection, the high freqs in circuit (E) just ripple along through the cap and show up "ACROSS" the (output) resistor.
In (A) and (D), the hi freqs "shunt" down through the cap; they are "low" "pass". (B) and (C) have no caps and therefore no frequency filtering performance compared to the rest.
Once-upon-a-time, all the EEs to be looked to us for this stuff! (They still DO in reality, so let's not let them down!)
|  | nitin
2006-10-30 01:51:34 | This question can be answered simply as follows:
In (E), the capacitor and resistor are connected in series. When driving frequency, f_d (equivalently angular frequence w_d), of V_{in} is high, the capacitive impedance X_C is small, so no voltage is dropped across the capacitance, and V_{out}=V_{in}. On the other hand, when f_d is low, X_C is high, and X_C>>R, so that almost all voltage is dropped across the capacitor. Hence, V_{out}\approx 0.
This is not the case for the other circuit arrangements. |  |
|
|
Comments |
casseverhart13
2019-09-24 06:06:16 | I must say, what a problem. Orlando Towing Partners - I-Drive |  | flyboy621
2010-10-24 16:07:24 | We can solve this without knowing anything about AC circuits.
First, you can eliminate the circuits with diodes, since neither would behave differently at different AC frequencies (why would they?). That rules out (B) and (C).
To narrow it down further, analyze the low-frequency limit, by assuming DC voltage (lowest frequency you can get, right?). We are given that 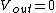 at low frequency. at low frequency.
(A) wouldn't work because the voltage across the capacitor, the resistor, and 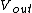 must each equal must each equal 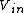 . .
(D) wouldn't work for a similar reason.
(E) is the only choice left. It looks like it would work because the capacitor would charge until the voltage drop across it equals 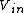 , and then there would be no more voltage drop across the rest of the circuit. , and then there would be no more voltage drop across the rest of the circuit.
We don't need to know the high-frequency behavior of any of these to know that (E) is right. |  | antithesis
2007-10-02 22:46:44 | A shortcut for this (and other filter problems) is to remember the following mnemonic: For RC, in a configuration such as that of figures D and E, the position of the capacitor determines the type of filter: If it it "up" (as in E), it is a high filter. If it is "low" (as in D), it is a low filter.
Then, remember that if you have LR, inductor is roughly opposite to a capacitor, so up means low filter, and vice versa.
I usually don't like to memorize useless stuff (I never took a real circuit course, with impudence), but this seems almost too trivial to remember. |  | Blake7
2007-09-23 05:50:32 | Folks, whenever you see the symbol for a cap, two parallel, UNCONNECTED lines, you should immediately think "DC 'Block'"; a "short". And, conversely, with a cap being a DC block, it is also an AC, Hi Freq "Pass". Go back and study Max's eqns for caps if you don't get this, yet.
So, by inspection, the high freqs in circuit (E) just ripple along through the cap and show up "ACROSS" the (output) resistor.
In (A) and (D), the hi freqs "shunt" down through the cap; they are "low" "pass". (B) and (C) have no caps and therefore no frequency filtering performance compared to the rest.
Once-upon-a-time, all the EEs to be looked to us for this stuff! (They still DO in reality, so let's not let them down!)
Blake7
2007-09-24 02:42:57 |
Ooooops!!!
A DC Block is an OPEN! A cap looks like an OPEN to DC! (not a short!) Pardon me!
At this point the physical intuition means more to me than the terms themselves.
Also, as far as the cap and the circuit are concerned, lower frequencies look closer to DC and therefore the GREATER their IMPEDANCE.
(Wow, Yosun, it might be nice if folks could edit their own comments.)
|
Blake7
2007-09-24 02:44:21 |
Ooooops!!!
A DC Block is an OPEN! A cap looks like an OPEN to DC! (not a short!) Pardon me!
(At this point the physical intuition means more to me than the terms themselves.)
Also, as far as the cap and the circuit are concerned, lower frequencies look closer to DC and therefore the GREATER their IMPEDANCE.
(Wow, Yosun, it might be nice if folks could edit their own comments.)
|
|  | nitin
2006-10-30 01:51:34 | This question can be answered simply as follows:
In (E), the capacitor and resistor are connected in series. When driving frequency, f_d (equivalently angular frequence w_d), of V_{in} is high, the capacitive impedance X_C is small, so no voltage is dropped across the capacitance, and V_{out}=V_{in}. On the other hand, when f_d is low, X_C is high, and X_C>>R, so that almost all voltage is dropped across the capacitor. Hence, V_{out}\approx 0.
This is not the case for the other circuit arrangements. |  | yosun
2005-11-11 13:41:15 | keflavich: the parser-error has been manually fixed, and i'd hopefully get to look at the code later this week to permanently fix it. (apparently, the symbol V_{in} confused it.)
high freq filters (as with low freq filters) are pretty easy. once u find the impedance, just take the right approximation in the particular regime you're interested in... and you're done. see above. |  | keflavich
2005-11-11 12:02:11 | Just a heads up: there appear to be a lot of HTML tags in your equations.... unless those 's are supposed to be there.
I don't know a thing about high-pass filters, but since an 'empty' (uncharged) capacitor lets all the current through and a full one lets none, E is the option that allows high-frequency current through but not low frequency. That's probably what you said, give or take, but I couldn't read it too well. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
