|
GR9677 #37
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
mpdude8
2012-04-20 14:22:44 | Yeah, I took the logic approach to this one as well. To someone standing watching this happen, the velocity of the new particle must be somewhere between 0.6c and 0.9c, and you can eliminate E because, come on, adding velocities in relativity is never that easy.
jdbro
2014-10-23 18:37:24 |
nice
|
|  | nirmalpratheep
2010-11-06 19:49:31 | 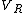 = =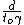 , ,
where 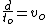
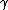 =5/4 =5/4
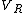 = =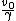
Therefore, 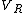 =0.6*(4/5)=0.48c; =0.6*(4/5)=0.48c;
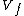 = =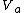 + +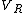 =0.48c+0.3c=0.78c =0.48c+0.3c=0.78c 0.76c(D) 0.76c(D) |  | Albert
2009-10-22 16:18:41 | Relativity is so glamorous! I love it.
Thank you, dear uncle Albert :)
|  | spacebabe47
2007-09-23 07:43:14 | Or, if you can't remember the formula, but you have seen any SR before you should know that the speed of the emitted electron will be greater than the atom (0.3 c) because they are traveling in the same direction, greater than the electron's speed in the rest frame of the atom (0.6c) because it is in a moving frame relative to the lab, but less simply adding the velocities (0.3c+0.6c=0.9c). This eliminates A,B, and E. A frame moving at 0.3c is fast enough to have a measurable impact on the velocity of the electron, so 0.76 seems more reasonable than 0.66c. Pick D.
sirius
2008-11-06 22:51:34 |
haha, sadly this is my typical approach to relativity. it's never the classical expectation, and its always faster than either of the particles alone. I nearly always choose the one thats slightly less than adding the two velocities. If only I had a better professor and a better text when I learned this stuff.
|
Kabuto Yakushi
2010-09-07 15:18:48 |
A good solution..Albert would be so disappointed! LOL
|
aprilrussell
2018-05-30 03:43:14 |
Relativity is so glamorous! I love it. \r\nhttps://run2.online/run-3
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
