|
GR9677 #36
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
CaspianXI
2009-03-22 16:24:17 | The two lumps' energies will be "converted" into mass when they collide and stop because we're given that no energy is radiated. Hence, the final mass must be greater than 8 kg. So, we can immediately eliminate options (A), (B), and (C).
So, if you can't figure it out, you can guess and have a 50% chance of getting it right. |  | lowder.chris
2007-10-03 21:31:57 | Relativity gives me a headache. :)
bbaker03
2007-10-16 18:38:25 |
sorry im looking at the solution and getting confused. are you using the equation 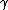 = = 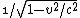
|
grae313
2007-10-31 12:44:17 |
yes, bbaker03, if you plug in 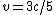 to the equation you wrote for gamma, you get to the equation you wrote for gamma, you get 
|
bbaker03
2007-11-01 10:24:11 |
Thanks a lot for your help this site is saving my life on this test. Can't thank you all enough.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
