|
GR9677 #3
|
|
|
|
|
Alternate Solutions |
jmason86
2009-09-28 18:37:55 | Don't even both with anything more than the distance. All the answers are identical except for the dependence on R and x which are the distances. You know that 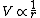 so just get r. so just get r.
Draw the triangle and see that (B) does the job. |  | spacebabe47
2007-09-19 13:39:58 | As R -> 0, the equation should simplify to the potential for a point charge. This eliminates C, D and E. The equation should also have some R dependence, this eliminates A. Choose B. |  | sblusk
2006-10-24 06:14:40 | An alternate way would be to just use directly:
V(r) = Integral (1/4*(pi*e_0))* dQ/r
where r=sqrt(R^2+x^2).
This is in principle easier because one is dealign with a scalar, and not the electric field which is a vector. |  |
|
|
Comments |
fredluis
2019-08-08 06:54:37 | After the binomial expansion, the potential should have a \"-\" instead of a \"+\" in the expansion term. However, a minus exists in the force equation because the test charge has charge -q. tile contractor |  | sean9
2017-11-28 08:41:44 | When x = 0, the answer is just that of a point charge Q at distance R.\r\njson formatter\r\n |  | curious_onlooker
2017-10-25 19:59:53 | When x = 0, the answer is just that of a point charge Q at distance R. You can see this at a glance because the integrand (if you wrote it out) would not have any position dependence (all dq\'s are the same distance from where we\'re evaluating the potential). When x is non-zero but R = 0, the answer should also be that of a point charge but with distance x. The only answer satisfying this is B. |  | Laxrabi23
2017-10-16 12:58:32 | I thought I could get to see and discuss all released GRE questions in here, but I can only see discussions about the four old question papers. Are only those discussed here or am I not able to find discussions about recently asked questions? Please someone make me clear about it. Thanks,,\r\n |  | jmason86
2009-09-28 18:37:55 | Don't even both with anything more than the distance. All the answers are identical except for the dependence on R and x which are the distances. You know that 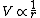 so just get r. so just get r.
Draw the triangle and see that (B) does the job. |  | spacebabe47
2007-09-19 13:39:58 | As R -> 0, the equation should simplify to the potential for a point charge. This eliminates C, D and E. The equation should also have some R dependence, this eliminates A. Choose B.
ewhite2
2007-10-30 17:32:36 |
how is C eliminated?
|
kyros
2007-11-01 10:40:09 |
C isn't eliminated that way -but it's clear that at x = 0, the answer should be non-zero(consider a positive charge and positive Q, the integral from infinity to zero can't be zero.)
|
ghost2k15
2017-08-27 01:13:21 |
How does that eliminate C?
|
ghost2k15
2017-08-27 01:14:12 |
sorry was on a half screen and didn\'t see the comments
|
|  | sblusk
2006-10-24 06:14:40 | An alternate way would be to just use directly:
V(r) = Integral (1/4*(pi*e_0))* dQ/r
where r=sqrt(R^2+x^2).
This is in principle easier because one is dealign with a scalar, and not the electric field which is a vector. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
