|
GR9677 #29
|
|
|
|
|
Alternate Solutions |
ticklecricket
2010-11-11 19:52:37 | It is worth noting that G has kg in the denominator and that h has kg in the numerator (1 Js = kg m^2/s) so only choices A and E will properly cancel out kg. So you don't even have to worry about B, C, and D |  | Herminso
2009-09-21 11:48:54 | Since by definition the Planck length is in meters, and knowing from the answers that the correct choice must contain 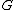 , , 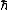 , and , and  : :
![[m]=[G^{\alpha}\hbar^{\beta} c^{\gamma}]=\frac{m^{3\alpha}}{Kg^{\alpha}s^{2\alpha}}\frac{Kg^{\beta}m^{2\beta}}{s^{\beta}}\frac{m^{\gamma}}{s^{\gamma}}](/cgi-bin/mimetex.cgi?[m]=[G^{\alpha}\hbar^{\beta} c^{\gamma}]=\frac{m^{3\alpha}}{Kg^{\alpha}s^{2\alpha}}\frac{Kg^{\beta}m^{2\beta}}{s^{\beta}}\frac{m^{\gamma}}{s^{\gamma}})
That imply:
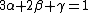 , ,
 , ,
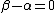 . .
Solving that equations: 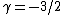 , , 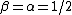 . .
|  |
|
|
Comments |
dreamweaves
2017-10-18 22:59:07 | Quickest way to do this one is to look at the units of G, h, and c. All of these constants have units of inverse time, so there has to be division somewhere to eliminate the time component. E is the only option with division. It has to be the correct answer by process of elimination. |  | buaasyh
2015-09-30 12:47:45 | A quantum effect may emerge within very small scale, so the light speed c=299792458 m/s may locate in the denominator. \r\n \r\n / |\r\n \\ -------/------/\r\n<||:-)) |---< |\r\n / ------ \\------\\\r\n \\ | |  | ticklecricket
2010-11-11 19:52:37 | It is worth noting that G has kg in the denominator and that h has kg in the numerator (1 Js = kg m^2/s) so only choices A and E will properly cancel out kg. So you don't even have to worry about B, C, and D |  | phoxdie
2010-11-09 09:55:56 | In addition to barefooto's post, it is a bit suspicious that choices A-D all have the same form while E stands out. If I saw a problem like this on my test and was seriously crunched for time it may be worth guessing the one answer which stands out. I can't tell if the GRE writers intentionally do this type of thing, but I have noticed other problems were this is a valid strategy for quickly answering problems. |  | phoxdie
2010-11-09 09:55:56 | In addition to barefooto's post, it is a bit suspicious that choices A-D all have the same form while E stands out. If I saw a problem like this on my test and was seriously crunched for time it may be worth guessing the one answer which stands out. I can't tell if the GRE writers intentionally do this type of thing, but I have noticed other problems were this is a valid strategy for quickly answering problems. |  | phoxdie
2010-11-09 09:55:26 | In addition to barefooto's post, it is a bit suspicious that choices A-D all have the same form while E stands out. If I saw a problem like this on my test and was seriously crunched for time it may be worth guessing the one answer which stands out. I can't tell if the GRE writers intentionally do this type of thing, but I have noticed other problems were this is a valid strategy for quickly answering problems. |  | Herminso
2009-09-21 11:48:54 | Since by definition the Planck length is in meters, and knowing from the answers that the correct choice must contain 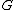 , , 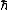 , and , and  : :
![[m]=[G^{\alpha}\hbar^{\beta} c^{\gamma}]=\frac{m^{3\alpha}}{Kg^{\alpha}s^{2\alpha}}\frac{Kg^{\beta}m^{2\beta}}{s^{\beta}}\frac{m^{\gamma}}{s^{\gamma}}](/cgi-bin/mimetex.cgi?[m]=[G^{\alpha}\hbar^{\beta} c^{\gamma}]=\frac{m^{3\alpha}}{Kg^{\alpha}s^{2\alpha}}\frac{Kg^{\beta}m^{2\beta}}{s^{\beta}}\frac{m^{\gamma}}{s^{\gamma}})
That imply:
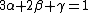 , ,
 , ,
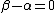 . .
Solving that equations: 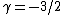 , , 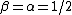 . .
|  | eshaghoulian
2007-10-02 04:21:34 | I like barefooto's remark. It seems as if for most of the dimensional analysis problems you can pick a unit (sometimes kg, in this case meters) and see what combination will eliminate it. In this case, even if you didn't pick meters and picked kg, then all but A and E would be eliminated. You have to be careful with the meters argument, though; you could conceive of three constants with units  , and , and 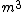 , stack them all next to each other, and take it to the 1/7th power at the end. So it's not necessary, in general, that one of the constants be on the bottom. But it's definitely the cleaner approach in this problem, as only choice E takes the terms to a root. , stack them all next to each other, and take it to the 1/7th power at the end. So it's not necessary, in general, that one of the constants be on the bottom. But it's definitely the cleaner approach in this problem, as only choice E takes the terms to a root.
evanb
2008-06-30 13:38:24 |
Yes, a safer choice is to track seconds.
[G] is m^3 / kg s^2
[h] is J s which is kg m^2 / s
[c] is m/s.
We MUST eliminate seconds, so there must be a division in our answer.
Thus, the answer is E.
|
|  | barefoot0
2006-11-02 14:06:48 | Because all three constants have meters in the numerator you can rule out any answers that do not have at least one constant in the denominator and on in the numerator.
This gives you a shortcut to the correct answer with a bit less work. |  | gatboja
2005-12-08 12:48:39 | trivial comments:
A: has m^6/s^4
C: has m^9/(kgs^6) |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
