|
GR9677 #27
|
|
|
Problem
|
|
|
This problem is still being typed. |
Lab Methods }Log Graphs }Log Graphs
Log graphs are good for exponential-related phenomenon. Thus (A), (C), and (E) are appropriate, thus eliminated. The stopping potential has a linear relation to the frequency, and thus choice (B) is eliminated. The remaining choice is (D).
|
|
|
Alternate Solutions |
Izaac
2012-08-21 01:18:44 | One can also simply remember that Bode plots (gain VS 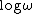 ) are semilog ones, so obviously D is inappropriate . ) are semilog ones, so obviously D is inappropriate . |  |
|
|
Comments |
Memol
2012-09-18 07:17:56 | Can anyone help me with an study reference about these graph stuff? |  | Izaac
2012-08-21 01:18:44 | One can also simply remember that Bode plots (gain VS 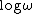 ) are semilog ones, so obviously D is inappropriate . ) are semilog ones, so obviously D is inappropriate . |  | keenanman
2007-10-16 12:38:05 | In choice D, the graph gain vs 1/frequency is linear. The graph gain vs frequency is hyperbolic. |  | eshaghoulian
2007-10-02 04:11:09 | Just to add a little bit as to why log graphs are good for exponential related phenomena, note that a power law in log-log coordinates is a line:
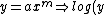 = log(ax^m) = mlog(ax) = mlog(x)+ mlog(a) \Rightarrow log(y) = mlog(x) + mlog(a)) which is of the form which is of the form 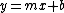 (since (since ) is just a constant (like is just a constant (like 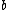 ) and we identify ) and we identify 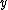 with with 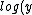) and and  with with ) , as these are our new axes in log-log coordinates). So the exponent in the power law becomes the slope in log-log coordinates. Testing this is a GRE favorite, as it is a major tool in experimental physics. , as these are our new axes in log-log coordinates). So the exponent in the power law becomes the slope in log-log coordinates. Testing this is a GRE favorite, as it is a major tool in experimental physics.
tachyon788
2009-10-06 11:48:47 |
You have a small math error in your use of logs. The equation should be:
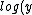=log(ax^m)=log(a)+log(x^m)=log(a)+mlog(x))
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
