bluejay27
2016-12-22 22:12:03 | Air is obviously less dense than the atomic radius 10^{-10}?? What does this mean?
blacksheep
2017-03-08 00:23:16 |
It took me a second to grasp her meaning, too. She\'s just saying that obviously air molecules at a normal density (\"room conditions\") aren\'t packed into a volume of space with literally no room between molecules. The scale (the \"size\") of atoms and molecules is on the order 10^-10 meters (whereas atomic nuclei are on the scale of 10^-14 meters or so), so the \"packing\" of air molecules in the volume of space has to be on a higher scale or else they couldn\'t move at all. Since mean free path has to do with the distance air molecules travel between collisions, it too has to be on a higher scale. Only answers A and B satisfy this requirement.
|
|  |
Bacon
2012-09-27 18:18:32 | Number density = # atoms per volume (or N/V). From ideal gas law PV=NkT we get N/V = P/kT.
The cross section is pi*r^2. One should know the radius of an atom is on the order of one angstrom, so say r = 10^-10. Therefore, the cross section (call it A) is A = pi*10^-20, or just 10^-20.
As for the number density N/V = P/kT, plug in standard pressure/temp values (10^5 Pa and 300 K), combine it with the above area, and you'll get very close to the answer. |  |
wittensdog
2009-10-16 16:34:27 | I think the best strategy, if you want to do the numbers, having looked at all of the comments below, is to use two facts:
1.) an ideal gas takes up about 22.4 liters at normal room conditions
2.) a cubic meter is 1,000 liters
and then use a radius on the order of the Bohr radius. The first two pieces of information, when combined, say the number density should be about 3*10^25 for every cubic meter. Taking the Bohr radius as the radius of our molecules (which is kind of close), we get a cross sectional area of about 2.5 * pi * 10 ^ -21. Multiplying this and inverting gives on the order of (1/2) * 10^-8 , so we should choose B.
Having said that, I think it would be better to consider two things:
1.) the mean free path cannot be on the order of the Bohr radius or lower, because then the spacing between atoms would be on the order of their size, and we would be starting to end up with a quantum gas, far removed from how air behaves at normal room conditions
2.) the mean free path of air molecules should not start approaching the macroscopic range
This rules out everything except for B, and is pretty much what the original solution says.
I think the most important moral here to remember is that the characteristic spacing between air molecules is about 1,000 times larger than their characteristic size. |  |
gotfork
2008-07-12 15:28:34 | Again, just pointing out that the ohio state site cites this one as a source... |  |
bkardon
2007-09-30 09:19:42 | Here's how one might solve the problem:
Assuming air is an ideal gas,
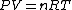
since 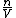 represents the molar density of the gas, represents the molar density of the gas,
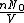 represents the number density, with represents the number density, with 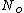 being Avogadro's number: being Avogadro's number:

using room conditions,
)
as given on the equation sheet
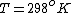
Once you approximate your way through the math, you arrive at
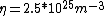
We can approximate the cross section of air molecules as 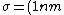^2) , or , or 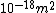 , so the mean free path is found to be , so the mean free path is found to be

This answer is closest to 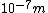 , so we can choose answer B. , so we can choose answer B. |  |
Richard
2007-09-26 12:59:02 | The diameter of an air molecule is ~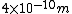
The number density of air is ~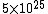 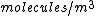
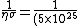(10\times 10^{-20})}=2\times 10^{-2} 10^{-5}=2\times 10^{-7})
So I guess you choose (B). |  |
Richard
2007-09-26 12:31:26 | Has anyone heard the Fermi atomic bomb story?
...these problems are appropriately called "Fermi Problems." |  |
warisit
2007-07-24 19:27:20 | What about this?
The density of air is
(6.02 * 10^23 # ) / (22.4 * 10^(-3) m^2 )
and,
assuming the size of 1 molecule is about 1nm,
the collision cross section is 1nm^2
Putting this value into the equation gives the answer
~10^(-7) m
|  |
RootMeanSquare
2006-11-19 02:15:33 | Common sense might require some time that we don\'t have in the exam, so...:
If you remember  and the mol volume 22.4 litres, you end up with a number density of rougly and the mol volume 22.4 litres, you end up with a number density of rougly 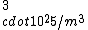 . With a guessed molecule radius of a little more than twice the atomic radius of . With a guessed molecule radius of a little more than twice the atomic radius of 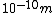 (hint: guessing (hint: guessing 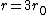 helps here:-)) you end up with helps here:-)) you end up with 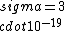 , which gets you right to solution (B) , which gets you right to solution (B) |  |
RootMeanSquare
2006-11-19 02:06:51 |
godkun1
2017-03-15 17:33:04 |
Just an empty????
|
|  |
scottopoly
2006-11-03 15:44:48 | I was going to recommend this site:
http://www.physics.ohio-state.edu/undergrad/ugs_gre.php />
but apparently Yosun has been copying solutions from there....
gotfork
2008-07-12 15:21:15 |
Wrong. The solutions there cite her site as the source.
|
sirius
2008-11-06 22:25:49 |
I'm pretty sure it's the other way around.
|
athithi
2009-12-09 23:16:57 |
its other way...they are copying from this website...just check properly..
|
Crandor
2010-04-09 19:27:22 |
Other way around.
|
dinoco
2010-11-01 07:46:38 |
I think that it was a joke.
|
godkun1
2017-03-15 17:32:25 |
you are completely right......this is really bad.....
|
|  |
radicaltyro
2006-11-02 17:31:06 | Apparently I don't have any common sense. Anyone with a real solution?
ali8
2011-07-18 05:25:19 |
Neither do I.
|
|  |
