|
This problem is still being typed. |
Electromagnetism }RC Circuit }RC Circuit
One can immediately eliminate plots A, C, E, since one would expect an exponential decay behavior for current once the switch is flipped.
More rigorously, the initial circuit with the switch 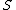 connected to connected to  has the following equation, has the following equation,
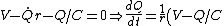<br />
)
Once integrated, the equation becomes,
<br />
)
The charge stored on the capacitor after it is fully charged is  (at (at 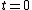 ). ).
When the switch 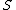 is switched to is switched to 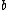 , the equation becomes, , the equation becomes,
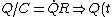 = Q_0 e^{-\frac{t}{RC}},<br />
)
where 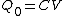 from the initial connection. from the initial connection.
Current is the negative time derivative of charge, and thus,
=-\dot{Q}=\frac{Q_0}{RC} Q(t) = \frac{V}{R}Q(t)<br />
)
The initial current IS =V/R) , and thus choice (B) is right. , and thus choice (B) is right.
|
