|
GR9277 #92
|
|
|
Problem
|
|
\prob{92}
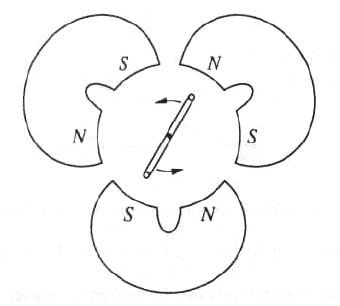
A flat coil of wire is rotated at a frequency of 10 hertz in the magnetic field produced by three pairs of magnets as shown above. The axis of rotation of the coil lies in the plane of the coil and is perpendicular to the field lines. What is the frequency of the alternating voltage in the coil?
- 10/6 Hz
- 10/3 Hz
- 10 Hz
- 30 Hz
- 60 Hz
|
Electromagnetism }Frequency }Frequency
A three-pole magnet should produce three voltage peaks, and thus the frequency is 30 Hz. (Solution due to David Latchman.)
|
|
|
Alternate Solutions |
dberger8
2016-08-20 21:00:10 |  , so the frequencies will be the same.We have 3 , so the frequencies will be the same.We have 3 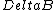 \'s (i.e. changing from N->S) per revolution, and we are rotating at 10 revolutions per second. So, multiply \'s (i.e. changing from N->S) per revolution, and we are rotating at 10 revolutions per second. So, multiply \\left(\\frac{3 \\Delta B}{rot.}\\right)) to get the frequency of the induced voltage. to get the frequency of the induced voltage. |  |
|
|
Comments |
dberger8
2016-08-20 21:00:10 |  , so the frequencies will be the same.We have 3 , so the frequencies will be the same.We have 3 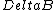 \'s (i.e. changing from N->S) per revolution, and we are rotating at 10 revolutions per second. So, multiply \'s (i.e. changing from N->S) per revolution, and we are rotating at 10 revolutions per second. So, multiply \\left(\\frac{3 \\Delta B}{rot.}\\right)) to get the frequency of the induced voltage. to get the frequency of the induced voltage.
Ryry013
2019-10-19 12:29:56 |
(Fixing the Latex)\r\n\r\n , so the frequencies will be the same. We have 3 , so the frequencies will be the same. We have 3 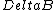 \'s (i.e. changing from N-->S) per revolution, and we are rotating at 10 revolutions per second. So, multiple \'s (i.e. changing from N-->S) per revolution, and we are rotating at 10 revolutions per second. So, multiple  \\left( \\frac{3 \\text{rot.}}{\\Delta B} \\right)) to get the frequency of the induced voltage. to get the frequency of the induced voltage.
|
Ryry013
2019-10-19 12:30:25 |
(Fixing the Latex)\r\n\r\n , so the frequencies will be the same. We have 3 , so the frequencies will be the same. We have 3 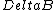 \'s (i.e. changing from N-->S) per revolution, and we are rotating at 10 revolutions per second. So, multiple \'s (i.e. changing from N-->S) per revolution, and we are rotating at 10 revolutions per second. So, multiple  \\left( \\frac{3 \\text{rot.}}{\\Delta B} \\right)) to get the frequency of the induced voltage. to get the frequency of the induced voltage.
|
Ryry013
2019-10-19 12:36:04 |
Man this site is buggy. Looked alright in the preview! Basically, it was V is proportional to dB/dt which is about equal to ΔB/Δt. There\'s 3 ΔB per revolution (as in, min-->max, changing from N-->S), so if we multiply (10 rotations/second)(3 ΔB/rotation) we get 30 ΔB/second
|
|  | mpdude8
2012-04-20 01:27:20 | Well, even if you didn't know the solution off the top of your head -- if you add more magnets, would you expect the frequency to increase or decrease? I'd expect it to increase, and since 3 * 10 was an option, I went with D.
Baharmajorana
2014-10-18 11:20:27 |
Hahah cool
|
|  | flyboy621
2010-10-23 04:59:23 | The field lines that start at a given N pole would terminate at each of the two neighboring S poles. By symmetry, the physics repeats 3 times per cycle. |  | tmansuripur
2008-10-17 22:20:50 | This problem is best solved by symmetry, without even thinking about the B-field lines. In fact, I think the problem is poorly described, and I don't exactly see where the magnetic flux is going through. Anyways, if you rotate the coil 120 degrees, then you're in exactly the same place (relative to the field lines) that you started at , so the voltagemust be the same as where you started at. Thus each full rotation of the rod corresponds to 3 cycles in the emf, so the voltage frequency is 3 times as large as the rotational frequency--->30Hz.
cartonn30gel
2011-04-06 23:28:46 |
I love this solution! It is so elegant but still very simple. Thanks for sharing it!
|
|  | thebigshow500
2008-09-13 21:10:49 | If you draw the magnetic field lines in the diagrams, you will see the field flowing from magnet's N pole to its own S pole. But I don't see how the voltage (or should we say current?) gets altered back and forth in the wire. Is the Lorentz force the one make the wire rotate?
Poop Loops
2008-10-25 20:16:00 |
*You* are rotating the wire at 10Hz and seeing what happens.
The voltage gets altered back and forth due to changing magnetic flux through the loop.
The picture is sort of misleading, but imagine that it isn't neat like that, but the magnets are smaller, so that magnetic field lines flow primarily from a magnet's own N to S (or whatever).
When the loop gets between the N and S poles, it has the greatest amount of flux going through it. So, as the loop approaches that point, flux goes up, creating a voltage, and then goes back down and negative as it starts going away.
Since there are 3 identical magnets spaced equally apart, this happens 3 times per rotation, so your frequency of whatever voltage waveform comes out gets tripled.
|
asdfuogh
2011-10-03 15:33:36 |
How come the field lines don't go to the other magnets? I mean, if we consider them not as horseshoe magnets, but just individual sources, wouldn't we see 6 fields, +>-, then ->+, then +>- again, and so on? Then as we rotate the coil, it'd switch 6 times per rotation, right?
Or is one AC rotation when it goes positive, then negative, and not just positive (or just negative)?
|
drunkphysics
2013-09-09 07:07:43 |
to asdfuogh,
I made this same mistake in judgement..
it does switch 6 times per rotation, but remember that frequency deals with 1 full sine wave of voltage. If the voltage peaks at N and troughs at S, then it will peak 3 times per rotation.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
