|
GR9277 #86
|
|
|
|
|
Alternate Solutions |
Herminso
2009-09-22 14:33:45 | The discharge of the capacitor after it has been charged to  is just is just
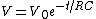  }) , ,
thus after the switch is opened, since  is in series with the capacitor we need to find is in series with the capacitor we need to find  , which we can determine by how fast the trace sweeps, s. We need to find , which we can determine by how fast the trace sweeps, s. We need to find  , will be given. Thus the answer is (B). The ration , will be given. Thus the answer is (B). The ration  can be read off the vertical parts of the scope. can be read off the vertical parts of the scope. |  |
|
|
Comments |
ehsana
2013-10-07 17:36:19 | Voltage through a discharging capacitor should be =V_0 e^{-t/RC}) . .
=V_0(1- e^{-t/RC})) , as it's written in the solution, is the voltage through a charging capacitor. , as it's written in the solution, is the voltage through a charging capacitor. |  | astro_girl
2013-09-13 06:30:48 | The voltage across the capacitor and acrossR, when the switch is closed, is not 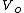 but but 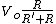 . When the switch is closed the capacitor branch is open , but current keeps flowing through R. This doesn't affect the answer though. . When the switch is closed the capacitor branch is open , but current keeps flowing through R. This doesn't affect the answer though. |  | flyboy621
2010-10-22 21:23:15 | You can do this one by elimination.
When the switch is opened, R' is out of the picture, which rules out (D). (E) is too vague to be meaningful, so that choice must be wrong. Finally, it should be obvious that  will affect only the scale of the scope display and not the time-behavior of it. Thus (A) and (C) are ruled out. (B) is the only choice left. will affect only the scale of the scope display and not the time-behavior of it. Thus (A) and (C) are ruled out. (B) is the only choice left. |  | Herminso
2009-09-22 14:33:45 | The discharge of the capacitor after it has been charged to  is just is just
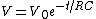  }) , ,
thus after the switch is opened, since  is in series with the capacitor we need to find is in series with the capacitor we need to find  , which we can determine by how fast the trace sweeps, s. We need to find , which we can determine by how fast the trace sweeps, s. We need to find 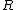 , will be given. Thus the answer is (B). The ration , will be given. Thus the answer is (B). The ration 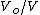 can be read off the vertical parts of the scope. can be read off the vertical parts of the scope. |  | oSciL8
2009-03-29 19:04:58 | Wait a minute - I thought the time constant (tau = 1/RC) was dependent on the resistor in series with the capacitor? This would mean that one would need to know the sweep rate and R', not R...would someone explain?
Thanks for this website btw - I'll see how helpful its been in a week!!
gt2009
2009-06-21 04:13:49 |
After the switch is opened, R is in series with the capacitor.
|
|  | hamood
2007-04-05 14:42:14 | Capacitor discharging is V = Vo )
Capacitor charging is V(t) = Vo(1-) ) )
grace
2010-11-10 22:50:28 |
I agree with you.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
