|
GR9277 #73
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
QuantumCat
2014-09-25 13:22:16 | 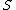 = = 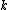 ln ln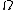
At any arbitrarily high temperature, the system only has two accessible states, so 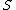 = = 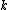 ln( ln(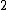 ). C is the only answer choice with this. ). C is the only answer choice with this.
The third law of thermodynamics says that the 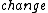 in entropy of a system approaches zero at absolute zero. Also because we cannot directly measure entropy, I think it is a bit of a misnomer to say that entropy is 0 at T = 0, but not according to ETS... in entropy of a system approaches zero at absolute zero. Also because we cannot directly measure entropy, I think it is a bit of a misnomer to say that entropy is 0 at T = 0, but not according to ETS... |  | Ami
2009-10-08 06:44:31 | the partition function is not as mantiond but:
) . .
carle257
2010-04-10 01:14:01 |
Why do we not just choose E1 to be zero? Simplifies things a bit.
|
flyboy621
2010-10-22 16:23:49 |
Ami,
You are correct, but it's simpler to set 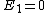 , which is perfectly OK and simplifies the algebra. Then , which is perfectly OK and simplifies the algebra. Then
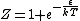
|
|  | le.davide
2009-10-05 00:03:34 | What about the degrees of degeneracy in the partition function?
Ami
2009-10-08 16:00:41 |
one for each energy level for each system...
what's wrong with that?
|
|  | Poop Loops
2008-10-25 17:38:11 | You can also look at this conceptually. Remembering that 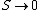 as as  , you already eliminate all but 2 choices. , you already eliminate all but 2 choices.
It's tempting to think that Entropy can increase indefinitely, but think about what's going on here. Say this system is a perfect gas. As temperature increases, so does entropy because everything is getting more and more disordered. But, at really high temperatures, every particle is already zooming around everywhere really fast, so you can't really get *more* disorder. |  | Imperate
2008-10-16 12:54:18 | A simple way to see that C is the correct answer is that at low temps all the subsystems reduce into the lowest state E_1, and thus the number of accessible microstates of the whole system is just one at abs zero (so S=klnW=kln(1)=0). But at arb high temps, each system is equally likely to be in E_1 or E_2, so you have a two level system (just like the isolated spin-1/2 paramagnet at high temps), and to find the microstates of the whole system it's like finding how many ways to arrange O's and X's on a checkboard with N places. Thus there are W=2^N microstates at high temps, and entropy is S=kln2^N=kNln2.
|  | sharpstones
2007-03-26 18:39:34 | Not to be too nitty gritty but ) . In our case at high T where Z = 2 then it reduces to the right answer. . In our case at high T where Z = 2 then it reduces to the right answer.
insertphyspun
2011-06-28 14:33:53 |
Yes, that was my problem with the original solution! Don't confuse the micro-canonical partition function with the canonical partition function (or the grand-canonical for that matter).
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
