GREPhysics.NET: GR9277 #51

GR9277 #51

Problem

GREPhysics.NET Official Solution

\prob{51}
A particle of mass m is confined to an infinitely deep square-well potential:
$<br /> V(x)&=&\infty,\;\;x\leq0,x\geq a \\<br /> V(x)&=&0,\;\;0\lt x \lt a<br />$

The normalized eigenfunctions, labeled by the quantum number n, are $\psi_n=\sqrt{\frac{2}{a}}\sin \frac{n\pi x}{a}$

For any state n, the expectation value of the momentum of the particle is

0
$\hbar n \pi/a$
$\hbar n \pi/a$
$2\hbar n \pi/a$
$\hbar n \pi/a(\cos n\pi - 1)$
$-i\hbar n \pi/a(\cos n\pi - 1)$

Quantum Mechanics $\Rightarrow$ }Momentum

The momentum operator in position space is given by $p = \hbar/ i \frac{\partial}{\partial x}$ .

Thus, given the wave function, one can calculate the expectation value as $\langle \psi_n | p | \psi_n \rangle = \langle \psi_n | \hbar/ i \frac{\partial | \psi_n \rangle}{\partial x}\propto \int_0^a \cos(n\pi x/a)\sin(n\pi x/a)dx =0$ , since sine's and cosine's are orthogonal over a whole period.

The answer is thus (A).

Alternate Solutions

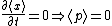carle257 2010-04-09 23:45:01	Also recall that the solutions when taken as pure states of only one n form stationary states of which the time derivative of all expecation values will be zero. Then $\frac{\partial \langle x \rangle}{\partial t}=0 \Rightarrow \langle p \rangle =0$ . Or just remember the momentum of a stationary state is zero. Reply to this comment
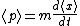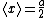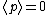radicaltyro 2006-10-30 23:17:29	As Griffiths says, "As Peter Lorre would say, Do it ze kveek vay, Johnny!'". $\langle p\rangle=m\frac{d\langle x\rangle}{dt}$ but $\langle x\rangle=\frac{a}{2}$ for the infinite square well, so $\langle p\rangle=0$ . Reply to this comment

Comments

carle257
2010-04-09 23:45:01

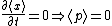Also recall that the solutions when taken as pure states of only one n form stationary states of which the time derivative of all expecation values will be zero. Then $\frac{\partial \langle x \rangle}{\partial t}=0 \Rightarrow \langle p \rangle =0$ . Or just remember the momentum of a stationary state is zero.

Reply to this comment

radicaltyro
2006-10-30 23:17:29

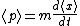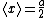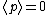As Griffiths says, "As Peter Lorre would say, Do it ze kveek vay, Johnny!'". $\langle p\rangle=m\frac{d\langle x\rangle}{dt}$ but $\langle x\rangle=\frac{a}{2}$ for the infinite square well, so $\langle p\rangle=0$ .

Reply to this comment

tera
2006-08-21 05:28:40

The expectation value of p is zero because otherwise the particle would tend either to go to the right or left and leave the well potential which is impossible!!!!!

Reply to this comment

jcain6
2005-11-22 18:58:36

The expectation value of p must be real. When the integral is set up, complex number i can be factored out to the front of the integral. With i in front of the integral the only way for the expectation value of p to be real is for the integral to produce imaginary numbers or for the integral to equal zero. Since there is no hope that the integral will produce complex numbers in this case the expectation value of p must be zero. Just a way to save a little time!

a19grey2
2008-11-02 11:13:07

Yeah, this is the fastest way for me to do it. Also, it applies more generally and it says that the expectation of the momentum will be zero any time that the derviative with respect to x doesn't bring out any factors of i.

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

1GHz Smartphone for 1 cent - best deal on a Samsung Galaxy Phone

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone