|
GR9277 #31
|
|
|
Problem
|
|
\prob{31}
In a 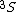 state of the helium atom, the possible values of the total electronic angular momentum quantum number are state of the helium atom, the possible values of the total electronic angular momentum quantum number are
- 0 only
- 1 only
- 0 and 1 only
- 0, 1/2, and 1
- 0, 1, and 2
|
Atomic }Spectroscopic Notations }Spectroscopic Notations
Spectroscopic notation is given by 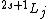 , and it's actually quite useful when one is dealing with multiple particles. , and it's actually quite useful when one is dealing with multiple particles. ) , respectively, for orbital angular momentum values of , respectively, for orbital angular momentum values of 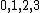 . . 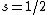 for electrons. j is the total angular momentum. for electrons. j is the total angular momentum.
Knowing the convention, one can plug in numbers to solve 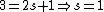 . Since the main-script is a S, . Since the main-script is a S, 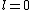 . The total angular momentum is . The total angular momentum is 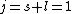 . .
|
|
|
Alternate Solutions |
eshaghoulian
2007-09-30 14:03:16 | Whoa. You have to be careful. Given 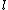 and and  ,the possible values of ,the possible values of 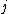 are, in general, j=l+s, l+s-1, l+s-2,...,|l-s|. Hund's rules tell you that are, in general, j=l+s, l+s-1, l+s-2,...,|l-s|. Hund's rules tell you that 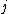 can only equal can only equal 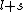 or |l-s|, depending on whether the subshell is more than half-filled. In this case, or |l-s|, depending on whether the subshell is more than half-filled. In this case, 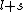 and |l-s| are the same number, so it does not matter. and |l-s| are the same number, so it does not matter. |  |
|
|
Comments |
deneb
2018-10-13 21:26:52 | I\'m confused what the answer is describing. Is the s=1 referring to the entire helium atom? This particular helium atom has two electrons which each have s=1/2, so together s=1? And then since it\'s in the S orbital, l=0, then j=1? |  | Poop Loops
2008-10-05 14:50:27 | So is s = 1/2 or s = 1? Two different "s"? I understand S = 0 because of 0 orbital angular momentum.
But does s refer to spin or what?
gear3
2013-10-09 05:48:01 |
the spin of Helium is 1.That's it
|
|  | bucky0
2007-11-01 14:09:11 | to clarify, the correct answer is B |  | eshaghoulian
2007-09-30 14:03:16 | Whoa. You have to be careful. Given 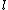 and and  ,the possible values of ,the possible values of 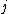 are, in general, j=l+s, l+s-1, l+s-2,...,|l-s|. Hund's rules tell you that are, in general, j=l+s, l+s-1, l+s-2,...,|l-s|. Hund's rules tell you that 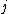 can only equal can only equal 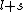 or |l-s|, depending on whether the subshell is more than half-filled. In this case, or |l-s|, depending on whether the subshell is more than half-filled. In this case, 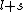 and |l-s| are the same number, so it does not matter. and |l-s| are the same number, so it does not matter.
Jeremy
2007-11-04 15:44:38 |
I don't think Hund's are involved in the solution. Hund's rules are only to determine the ground state, and problem isn't asking about that. I think the real point is that 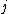 can be can be 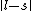 or any integer step above that, up to, and including, or any integer step above that, up to, and including, 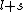 . In this case, . In this case, 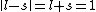 , so , so 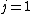 is the only option. is the only option.
|
DDO
2008-11-04 19:35:23 |
Jeremy that is Hund's 3rd rule.
|
iriomotejin
2010-10-06 08:42:25 |
Hund's rules deal with ground state, not with excited ones. The state of atom in this problem is obviously excited, so Hund's rules are irrelevant.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
