|
GR9277 #29
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
RusFortunat
2015-10-22 13:22:39 | \"An attractive, one dimensional square well\" I find it attractive too. |  | psychonautQQ
2013-11-28 15:39:39 | Is eliminating option A based on the fact that a bound state should go towards zero outside of the well correct?
RusFortunat
2015-10-22 13:30:14 |
Read first sentence from the top.
|
|  | maryami
2011-03-24 01:32:09 | in xx2 , the wave decays as E<0 and in x1
maryami
2011-03-29 15:05:17 |
so sorry, I don't know why it is typed incomplete,I 'm not familiar with the format of Latex
|
|  | e2ka
2009-10-05 13:42:14 | "Tunneling should show exponential decay for a finite-potential well, and thus choice (E) is eliminated"rnrnIs function E not demonstrating exponential decay for x < x1, x > x2? It looks to me like 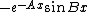 . There must be a better explanation for eliminating E. . There must be a better explanation for eliminating E.
kroner
2009-10-05 14:32:34 |
The behavior in (E) isn't really exponential decay. It's oscillating, and although the oscillations seem to decay, that's not the behavior exhibited in tunneling.
If you're looking for more detail about the physics behind that, the gist of it is that in the region outside the well, the eigenstates have to satisfy ![\psi^{\prime\prime}(x) = [-2m(E - V)/\hbar^2]\psi(x)](/cgi-bin/mimetex.cgi?\psi^{\prime\prime}(x) = [-2m(E - V)/\hbar^2]\psi(x)) where where  < < 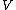 . That has solutions of the form . That has solutions of the form 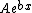 where where 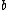 is strictly real. is strictly real.
|
|  | eshaghoulian
2007-09-22 16:38:58 | Choice D is eliminated more rigorously by invoking the property that the derivative of a wavefunction need be continuous (except at infinite potentials). This wavefunction is not even differentiable at 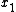 and and 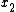 . .
RusFortunat
2015-10-22 13:18:57 |
yep
|
|  | Ingrid
2006-03-30 15:29:23 | Choice (A) is easy to rule out because the wave function should tend to sero for x-> +/-infinity.
zaijings
2009-03-13 19:23:52 |
you are right.
|
Plantis
2010-04-03 16:28:46 |
I think that (A) is correct answer too. What differnce between (A) and (B). I think - no difference.
|
raevyn
2010-04-08 13:40:31 |
Plantis, choice (A) does not go to zero at the "tails" (for 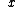 < < 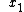 and and 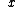 > > 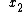 ) )
|
shak
2010-08-29 15:55:08 |
right
|
Crand0r
2010-11-12 18:39:13 |
On the other hand, wavefunctions are often drawn on pictures as if the "0" were the corresponding energy level. Given that, I think the question was poorly written.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
