|
GR8677 #86
|
|
|
Problem
|
|
 |
Electromagnetism }Coulomb's Law }Coulomb's Law
(Better classified as the Cavendish-Maxwell Experiment to determine the exponent in Coulomb's Law.)
One wonders why the common sense (and much too trivial) answer, choice (D), isn't right. In searching through one's lower level textbook, one would find accounts of Cavendish's Torsion experiment, which seems to also support choice (D). However, reading up on papers, one finds that the precise determination of the exponent is actually done via a whole different method... which although is an experimental technique, actually serves to illuminate the necessity of the inverse square law---and thus, this problem is not classified as a Lab Technique problem.
Charge up a conducting shell. Put a charge inside, distinctly asymmetrically far from the center but not touching the outer shell. One finds that the charge will not move.
This suggests that the field is 0.
Suppose that the field contribution to the test charge can be broken down into two unequal parts, set apart by a plane through the test-charge. 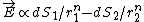 . Substituting the solid angle . Substituting the solid angle 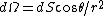 , one finds that , one finds that ) . Since the field vanishes for any . Since the field vanishes for any  , ,  , one deduces that , one deduces that 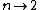 . .
For other and more modern methods, see page 95ff, especially page 100 of 
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
kiselev
2011-03-30 10:42:10 | I got this wrong, I thought that since perfect conductors doesn't exist (E) couldn't be the answer...I guess I'm wrong. What about the neutrality of charge of an atom? |  | yageda01
2009-07-28 12:28:24 | The electric field inside a conductor is zero, and by Gauss law this means 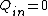 . .
From Electromagnetic fields (Wangsness), "this was first shown experimentally by Faraday in his famous "ice pail" experiment in which he measured the charge distribution on an ordinary metal pail."
Further...
"In fact, this conclusion forms the basis for the most accurate experimental tests of the exactness of the exponent 2 in Coulomb's law, since the experiments essentially look for deviations from the prediction 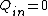 ; the results show that the exponent is indeed equal to 2 to within a few parts in ; the results show that the exponent is indeed equal to 2 to within a few parts in 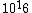 |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
