casseverhart13
2019-09-06 05:46:42 | Thank you a bunch for sharing this with all people you actually know what you are talking approximately! Bookmarked. house painting
danielsw98667
2019-10-21 06:33:35 |
Well, with the application of Gauss law the answer should be D. Villa Las Rocas
|
|  |
gigadan
2013-09-29 13:10:15 | How about we treat it as a dipole with d distance separation?
Then we know for sure answer has to contain qd
Also, the field of a dipole goes off by r^-3
gigadan
2013-09-29 13:12:39 |
I meant separation of 2d
So.. the 4pi would become 2pi as a result.
|
|  |
walczyk
2012-11-07 15:57:22 | The official solution is very good except that it starts off with the wrong sign. The term with (z-d) is the original charge, and (z+d) is the mirror charge [remember, if you increase z you should move closer to the original charge], and we also are given that the particle has charge -q. Therefore the problem is missing a factor of -1, which explains the negative charge density given in the solution. |  |
mpdude8
2012-04-19 15:06:22 | Dimensional analysis is your best friend on a 100 question exam. |  |
nakib
2010-04-02 08:40:10 | For grounded conductor 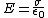 . .
By symmetry of the problem [remember that you have an opposite 'image' charge at -d],

Figure out  . Choice (D) is the answer. . Choice (D) is the answer.
But one need not go through all these if (s)he notes that only (D) has the right units. |  |
kroner
2009-10-05 23:28:58 | The conducting plate shields the far side from the electric field of the point charge so the field there is zero. On the near side close to the plate the parallel components are zero, and the perpendicular component should be double what's contributed by the point charge alone. So the field on the near side is
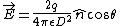
where  is the angle from the perpendicular so is the angle from the perpendicular so  . .
Applying Gauss's Law on a volume that contains a small area 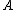 of the plate, of the plate,
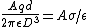 . .
|  |
proctort
2009-10-05 12:49:16 | What is " is the direction of the directest straight line" supposed to mean?rnIs "directest" even a word? is the direction of the directest straight line" supposed to mean?rnIs "directest" even a word? |  |
irishroogie
2007-10-04 18:31:37 | As erc pointed out, choice D is the only one with the correct units of charge over area.
ramparts
2009-11-05 15:20:12 |
You can do this the hard way, or you can do this the smart way. Unfortunately, yosun's answers, while a huge help, are often far more complicated than they need be, and not particularly amenable to a 100-question multiple-choice test.
|
|  |
RootMeanSquare
2006-11-25 11:50:18 | ?? I don't quite get the setup of this problem. lets say the plane lies in the xy plane, the V(0) = V(Z=0) or what? And in which direction is D supposed to point?
Sorry if this very stupid, but I really don't get the problem (aside from the imension analysis...) |  |
eigenrosen
2006-10-27 12:22:42 | And you can only combine the terms from the derivative after you plug in z=0 (the only place we would expect a surface charge).
tfw15
2008-10-10 19:26:00 |
Yeah the answer to this question definitely needs to be rewritten!
|
|  |
eigenrosen
2006-10-27 12:12:25 | I think the signs of the charges are off in the potential (given the assumption that the negative charge in the problem is in the +z direction, which you make when you take the normal derivative in the +z direction). This should account for the sign difference with the answer. |  |
l3amm
2006-10-19 20:02:59 | Alternatively, the only answer with the correct units is D. Simple, but little tricks can make hard problems really easy. |  |
erc
2005-11-05 11:20:57 | My reasoning was that (D) was the only one where the combination of d's and D's gave something with units of a surface density.
Plantis
2010-04-06 11:49:19 |
Absolutly correct! I agree.
|
shak
2010-07-31 13:15:29 |
Compare answers with their units...all are eliminated except D which has unit of charge over area
|
|  |
