|
GR8677 #52
|
|
|
|
|
Alternate Solutions |
jondiced
2010-10-18 18:22:29 | In the vein of what others have said, I thought about the boundary conditions.
Opposite sides of the cube have the same potential, so as we go across the cube we start with the potential at V and end with the potential at V. Since there are no charges inside, there is nothing to change the potential so it must be constant all the way across. |  | Herminso
2009-08-30 15:58:04 | An easier & faster way to do this problem is find the potential at the center of the cube as the average of the potential on the six sides, then it is V.
That can be generalized to any regular polyhedron with n sides (n=4,6,8,12,20), the n surfaces can be at different potentials Vi. The potential at the center of the polyhedron is the average of the potential on the n sides (see Jackson 3ed pag 94). |  | DaveyClaus
2006-11-17 05:10:14 | One cannot use Gauss's Law to determine 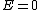 within. Only spherical and cylindrical Gaussian surfaces (and "pillboxes") allow one to take E out of the integral; we cannot automatically assume that within. Only spherical and cylindrical Gaussian surfaces (and "pillboxes") allow one to take E out of the integral; we cannot automatically assume that 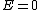 because because 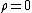 in this situation. in this situation.
 Instead, we simply recall that Laplace's equation, Instead, we simply recall that Laplace's equation, 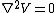 , with boundary conditions specified allows no maxima or minima within the boundary. So if the potential is V on the cube surface, potential cannot be greater than or less than V within. , with boundary conditions specified allows no maxima or minima within the boundary. So if the potential is V on the cube surface, potential cannot be greater than or less than V within.
 Now we are in a position to state that Now we are in a position to state that 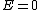 within... within... |  |
|
|
Comments |
fredluis
2019-09-17 01:57:42 | This is such an interesting solution i really like the way you solve it. carpet cleaners |  | ernest21
2019-08-23 02:02:41 | Why do they even bother? Even I won\'t like a life that complicated. robot battle games |  | Saint_Oliver
2013-09-12 18:46:31 | In the official solution, it is written 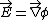 , but of course , but of course 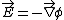 . This doesn't change much since . This doesn't change much since 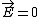 anyway, but it caught me off guard. anyway, but it caught me off guard. |  | Almno10
2010-11-11 21:54:25 | Imagine stretching cellophane tightly over a cactus, and a function describing the surface that ensues. That is laplace's equation at work.
Davey Claus is correct. Like the cellophane covered cactus, the maxima/minima of a potential occur only at the boundaries.
Laplace's equation says
"the simplest thing that can happen between the boundaries will."
|  | jondiced
2010-10-18 18:22:29 | In the vein of what others have said, I thought about the boundary conditions.
Opposite sides of the cube have the same potential, so as we go across the cube we start with the potential at V and end with the potential at V. Since there are no charges inside, there is nothing to change the potential so it must be constant all the way across. |  | alemsalem
2009-10-02 09:41:35 | the easiest way is to find a solution since we know it must be unique,, obviously a constant V in the cube satisfies both Laplace equation and the boundary condition
a62
2016-09-20 01:38:02 |
+1
|
|  | Herminso
2009-08-30 15:58:04 | An easier & faster way to do this problem is find the potential at the center of the cube as the average of the potential on the six sides, then it is V.
That can be generalized to any regular polyhedron with n sides (n=4,6,8,12,20), the n surfaces can be at different potentials Vi. The potential at the center of the polyhedron is the average of the potential on the n sides (see Jackson 3ed pag 94).
Herminso
2009-09-21 18:50:47 |
In LaTeX:

In our particular problem, 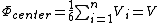 , since , since  on the six sides of the cube. on the six sides of the cube.
|
Herminso
2009-09-21 18:54:48 |
In LaTeX:

In our particular problem, 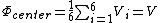 , since , since  on the six sides of the cube. on the six sides of the cube.
|
|  | Herminso
2009-08-30 15:52:35 | An easier & faster way to do this problem is find the potential at the center of the cube as the average of the potential on the six sides, then it is V.
That can be generalized to any regular polyhedron with n sides (n=4,6,8,12,20), the n surfaces can be at different potentials Vi. The potential at the center of the polyhedron is the average of the potential on the n sides (see Jackson 3ed pag 94). |  | phys2718
2008-10-16 16:29:33 | To elaborate on DaveyClaus:rnrnWe can "guess" a potential function of the form rnV(x,y,z) =  , where , where  is the potential on the boundary of the cube. Now we simply ask (1) Does this function satisfy Laplace's equaton? Answer: yes (2) Does this function satisfy the boundary conditions? Trivially, yes. Then we are guaranteed that we have found the unique solution to the problem.rnrnBy the way, I have been posting a lot of comments on this site and I should thank Yosun for creating it. With a lack of study books and resources for this test, I believe this website is extremely useful and beneficial for any student in preparation for the Physics GRE. is the potential on the boundary of the cube. Now we simply ask (1) Does this function satisfy Laplace's equaton? Answer: yes (2) Does this function satisfy the boundary conditions? Trivially, yes. Then we are guaranteed that we have found the unique solution to the problem.rnrnBy the way, I have been posting a lot of comments on this site and I should thank Yosun for creating it. With a lack of study books and resources for this test, I believe this website is extremely useful and beneficial for any student in preparation for the Physics GRE.
phys2718
2008-10-16 16:30:58 |
And of course the formatting screws up when I decide to thank Yosun for the website
|
|  | DaveyClaus
2006-11-17 05:10:14 | One cannot use Gauss's Law to determine 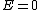 within. Only spherical and cylindrical Gaussian surfaces (and "pillboxes") allow one to take E out of the integral; we cannot automatically assume that within. Only spherical and cylindrical Gaussian surfaces (and "pillboxes") allow one to take E out of the integral; we cannot automatically assume that 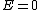 because because 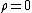 in this situation. in this situation.
 Instead, we simply recall that Laplace's equation, Instead, we simply recall that Laplace's equation, 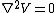 , with boundary conditions specified allows no maxima or minima within the boundary. So if the potential is V on the cube surface, potential cannot be greater than or less than V within. , with boundary conditions specified allows no maxima or minima within the boundary. So if the potential is V on the cube surface, potential cannot be greater than or less than V within.
 Now we are in a position to state that Now we are in a position to state that 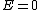 within... within...
spacemanERAU
2009-10-15 18:33:00 |
is a cube not a "pillbox"?
|
keyboarder
2010-05-07 18:35:08 |
spacemanERAU asked 'is a cube not a "pillbox"?'
A "pillbox" is most often used as a Gaussian surface at an interface between two different media. Since Gauss's Law applies for any arbitrary size of surface, the "pillbox" is made to shrink until it is of negligible size (infinitesimal): Either flat in one dimension or very small in multiple dimensions. Once it is small enough--especially near an interface--it is reasonable to assume that the E-field inside is symmetrical and/or constant throughout the pillbox.
The cube described in the problem is of finite size. Thus, it is not a pillbox in the context meant by DaveyClaus.
|
keyboarder
2010-05-07 18:49:19 |
It is worth clarifying that it is not only the choice of Gaussian surface which allows one to "take E out of the integral". The Gaussian surface is chosen to "match" the *charge distribution*. For example, choose a sphere with a spherically symmetric charge distribution, or a cylinder with a wire or coaxial (all with a common axis).
In other words, the symmetry of the Gaussian surface should match the symmetry of the charge distribution. This is what allows the flux integral to be simplified.
A spherical or cylindrical Gaussian surface will not help at all if the charge distribution (and hence, the E-field going through the Gaussian surface) has some other configuration.
|
padkins
2011-02-06 12:17:50 |
At first I thought you may be wrong, but here is a simple thought experiment that shows you must be correct:
Take a universe with no charge, draw a spherical gaussian surface. By symmetry (and of course cause there's no charge) there will be no field. This is of course the result given by the integral of the charge density within.
Now, do not change the charge density within (zero) and apply an external field from the outside; obviously the field at points on the sphere will be equal to whatever is given by the application of the field, but the gaussian integral will still be zero! Therefore, unless EVERYTHING in the problem exhibits spherical symmetry, the gaussian technique cannot be applied.
|
pam d
2011-09-24 12:04:42 |
Nice.
|
livieratos
2011-11-07 12:06:09 |
hmmm ok i might be wrong but as far as i know gaussian technique can be applied to every closed surface no matter what the shape and size of the surface. depending on the symmetry of the problem you take the easiest closed surface to help you with the calculations of the integral. with that in mind, in my opinion E = 0 inside the cube...
|
justin_l
2012-11-08 11:30:42 |
livieratosrnrnGauss's law is always "right", of course, but remember that the law involves the electric flux and the charge inside.rnrnAll Gauss's law says is that the total flux of the surface must be zero.rnrnHowever, just because the total flux is zero doesn't mean the flux doesn't vary across your surface. It could be a combination of E fields, all of which add up in the end to have zero flux.rnrnThe reason it applies to spheres is because the E field, from symmetry, must be spherically symmetric, so at every point on your surface, E must have the same magnitude. This is how you know that if your flux is zero, E must also be zero (because E is constant over your surface).rnrnIf you don't know that E is constant over your surface, you cannot assume that 0 flux implies 0 E at all places.
|
kronotsky
2018-10-23 04:29:06 |
This is not correct. The cube still has a symmetry, and we can apply Gauss\'s law in the same way as with a sphere as long as our integrals are over surfaces which respect that symmetry.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
