|
GR8677 #45
|
|
|
Problem
|
|
 |
Quantum Mechanics }Compton Effect }Compton Effect
This problem can be solved via the Compton Effect equation ) , where , where  is the angle of the scattered photon and is the angle of the scattered photon and 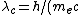) is the so-called Compton Wavelength. In this case, since the particles are protons, one has is the so-called Compton Wavelength. In this case, since the particles are protons, one has 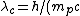) .
Since the photon scatters off at 90 degrees, the equation simplifies to .
Since the photon scatters off at 90 degrees, the equation simplifies to  . This is the increase in wavelength, as in choice (D). . This is the increase in wavelength, as in choice (D).
To a certain degree, one can hand-wave this problem via the following method:
Recall the de Broglie relation,

, where  is the wavelength, is the wavelength, 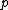 is the momentum and is the momentum and 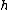 is Planck's constant. is Planck's constant.
The momentum of the proton is 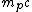 , thus , thus 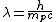 . .
|
|
|
Alternate Solutions |
OptimusPrime
2017-04-08 02:27:42 | (A) and (B) are maybes so far.\r\n(C) - No, we are dealing with PROTONS instead of the usual electrons. So the mass of the electron shouldn\'t come into play at all.\r\n(D) - Maybe.\r\n(E) - No, since after this collision the photon must lose energy. Recall that higher frequency means higher energy. So if we are losing energy, that means our frequency has decreased, and since frequency and wavelength are inversely related, the wavelength has increased. \r\n\r\nIf you remember the Compton equation then you\'ll find as Yosun wrote that change in wavelength equals the Compton wavelength. But, where can we extract any numbers from that?! We can\'t, so (A) and (B) are out.\r\n\r\nThat leaves (D). On top of that, (D) has the correct dimensions. [h/mc] = (M*(L^2) / T) / (M*L / T) = L. Length as in wavelength. |  |
|
|
Comments |
ernest21
2019-08-23 02:00:19 | When you say that by using energy to solve this, one would have to take into account the inertia, do you mean the rotational inertia of the rod? wordify |  | joshuaprice153
2019-08-09 06:19:20 | Thanks a lot for sharing us about this update. Hope you will not get tired on making posts as informative as this. appliance repair Orlando\r\n |  | OptimusPrime
2017-04-08 02:27:42 | (A) and (B) are maybes so far.\r\n(C) - No, we are dealing with PROTONS instead of the usual electrons. So the mass of the electron shouldn\'t come into play at all.\r\n(D) - Maybe.\r\n(E) - No, since after this collision the photon must lose energy. Recall that higher frequency means higher energy. So if we are losing energy, that means our frequency has decreased, and since frequency and wavelength are inversely related, the wavelength has increased. \r\n\r\nIf you remember the Compton equation then you\'ll find as Yosun wrote that change in wavelength equals the Compton wavelength. But, where can we extract any numbers from that?! We can\'t, so (A) and (B) are out.\r\n\r\nThat leaves (D). On top of that, (D) has the correct dimensions. [h/mc] = (M*(L^2) / T) / (M*L / T) = L. Length as in wavelength. |  | a62
2016-09-20 01:19:12 | I don\'t know the Compton equation off the top of my head, but I got this right easily simply because I remembered that the wavelength does change and the change is independent of the initial wavelength (I think that maybe that\'s important because it\'s predicted by the photon model, but not the classical wave model of light?). The wavelength shift is a result of a collision, so of course the mass in the equation is the mass of whatever the photon is colliding with. That narrows it down to only one answer. |  | 849444209
2013-10-16 06:29:20 | 记公式不就行了,这题太尼玛简单了
FloweryFlood
2014-10-05 04:49:25 |
Why are you always trying to be such arrogant?
What makes you feel like you are the only person who remember the equation:
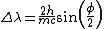)
|
godkun@yeah.net
2016-06-30 15:46:27 |
Don\'t be obnoxious!\r\n\r\n\r\n
|
|  | gigadan
2013-09-23 20:52:26 | How does a Photon have rest mass?
I was stumbled on C or D but D makes nonsense to me.
llama
2013-10-16 19:10:10 |
It doesn't, pRotons do :). D is the only one that deals with values relevant to the problem (well it's plausible that the fine structure constant is involved, but not immediately obvious)
|
|  | chrisfizzix
2008-10-03 12:45:53 | This problem bugged me a lot, mostly because I've been doing X-ray scattering problems in Solid State for several weeks now and had forgotten that elastic scattering didn't always imply that | | = | | = |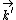 |... |...
< / whining > |  | Andresito
2006-03-16 21:29:44 | One should look at the important preposition "the wavelenght of scattered photons is INCREASED by"
This narrows the choices to (C) and (D), and one should choose (D) since it involves protons. The last argument merely goes as intuition.
ben
2006-07-18 16:59:11 |
this does not necessarily rule out (A) and (B) since lambda/137 and lambda/1836 are both positive numbers and adding them to the wavelength would still increase the wavelength. there is nothing inherently wrong with saying that the wavelength is increased by lambda/137. e.g., if the wavelength is 1 then increasing it by lambda/137 would give a wavelength of 1+1/137 which is greater than the original wavelength. no problem with that.
|
|  | jax
2005-12-02 11:13:45 | One thing I hate about the physics GRE is that I don't have time to derive things like the Compton equation from scratch... so the alternative is memorizing it but I am not very good at that. So if I happen to forget the equation, what do I do? Just skip the question, or spend 5 or 6 minutes deriving the equation.
My physics program never put the emphasis on what you could memorize so this type of exam is very hard for me to study for...
yosun
2007-02-22 15:23:21 |
The Compton Equation is actually one of those things you should know... (some even consider it a fundamental equation of modern physics) But, you can always derive it using conservation of momentum/energy.
|
jw111
2008-09-01 00:32:20 |
Try this.
All you need to know is
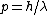
and
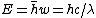
From the conservation of momentum and energy, we have
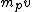 ~ ~ 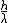
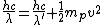
P.S. You may find out these two arguments by drawing yourself a simple sketch of vectors.
Substitution (1) into (2)
we have
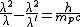
then, suppose 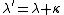
=\frac{h}{m_pc})
then
}})=\frac{h}{m_pc})
thus
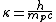
which  is the increasing of wave length is the increasing of wave length
Does this solve your problem? This is how I do this question.
The key idea of this method is that when writing down the energy conservation you can see both  and and 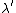 is is  in both sides of the equation. (How wonderful if you can subtract in both sides of the equation. (How wonderful if you can subtract  from from 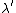 . That is the answer. The only difficulty is that they all at denomintors) Thus, you want to write . That is the answer. The only difficulty is that they all at denomintors) Thus, you want to write  as something big + something small. Then you can cancell the big ones on both side and the small one-the answer-remain. as something big + something small. Then you can cancell the big ones on both side and the small one-the answer-remain.
|
|  | physicsDen
2005-11-09 21:42:11 | how can the momentum of the PROTON have momentum with the speed of light???
yosun
2005-11-09 22:21:48 |
sorry physicsDen. that was a poor attempt to derive the compton effect from scratch. the standard method for solving that (i.e., the usual compton effect equation) has been posted. thanks for pointing this out. on the same tangent, you might be interested in:
http://grephysics.net/disp.php?yload=prob&serial=2&prob=67
|
|  | physicsDen
2005-11-09 21:40:52 | |  | physicsDen
2005-11-09 21:40:42 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
