GREPhysics.NET: GR8677 #40

GR8677 #40

Problem

GREPhysics.NET Official Solution

Advanced Topics $\Rightarrow$ }Radioactivity

Radioactive counting rates (number of decay per unit time) follow the Poisson Distribution. (Recall that the Poisson Distribution describes the results of experiments in which one counts events that occur independently, thus at random, but at a definite average rate.) In the PD, $\sigma=\sqrt{\bar{x}}$ , i.e., the standard deviation is approximately the square-root of the average.

Suppose $9934\approx 10000$ is the average. The square root of that is $100$ , hence (A) is the answer.

(Depending on whether one is in the mood for rolling the celestial self-loaded 5-sided dice, one can look for the most obvious relationship between numbers in problems. $\sqrt{x}, x^2$ are two commonly used relationships.)

The Normal (Gaussian) distribution describes the distribution of values for any measurement subject to many sources of error that are all random and small. But, the Poisson Distribution fits this case more closely.

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

joshuaprice153
2019-08-08 04:24:11

Hello there! This is my first comment here, so I just wanted to give a quick shout out and say I genuinely enjoy reading your articles. Can you recommend any other blogs/websites/forums that deal with the same subjects? Thanks. panel installation

Reply to this comment

casseverhart13
2019-08-06 08:59:25

I love the way you show your problem to us. Two thumbs up!!!! click here

Reply to this comment

walczyk
2011-04-06 22:36:51

how is the number of counts also the average? It seems like magic to me..oh wait i see it. you just say "counts per hour" and then it becomes an average. Its tricky because it doesn't tell you what time scale the average should be in. Weird problem.

Reply to this comment

spacemanERAU
2009-10-15 12:14:24

Im not smart so I was wondering if there was a way for non-intelligent people to solve this problem? I would have had the normal SD equation memorized and been lost as to how to use it to solve this problem. Any help is greatly appreciated.

ramparts
2009-10-30 15:28:46

Counting problems use the Poisson distribution, and the error scales as 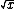$\sqrt{x}$ . Just something you've gotta memorize :) Maybe from your freshman physics lab, as it was for me.

mpdude8
2012-04-15 21:41:44

I, personally, like to see problems where I get almost no information in the question. You know, then, that the answer has to be something simple, or something purely based on logic and reasoning.

The only "number" you're given is 9934. Even if you forget the relationship given in the original solution above, you might try the square root as a guess. This yields a result suspiciously close to 100.

Not even a physical or mathematical argument -- but with only 90 seconds allotted per question, sometimes you have to try a clever guess.

justin_l
2012-11-08 11:05:14

Basically, whenever you see standard deviation in statistics/counting, you should see Square Root of N. Standard deviation is ALWAYS related to the square root of n in counting problems, and it's always associated with square roots in general.

Any time you see standard deviation, think square root.

Specifically if it's a counting problem.

Reply to this comment

erc
2005-11-05 08:01:34

Typo alert: 9934 ~ 10000 - too many zeros in solution.

yosun
2005-11-05 23:12:47

Thanks erc for the correction!

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone