|
GR8677 #19
|
|
|
Problem
|
|
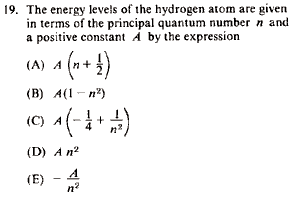 |
Quantum Mechanics }Bohr Theory }Bohr Theory
Recall the Rydberg energy. QED
|
|
|
Alternate Solutions |
casseverhart13
2019-10-01 03:22:05 | Good Examine and fascinating. Thanks. www.trustytreeservice.com |  | jeka
2007-02-17 08:08:36 | Energy spectrum of the hydrogen atom is given by the equation
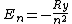 , ,
where 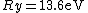 is the Rydberg constant. So the right answer is (E) is the Rydberg constant. So the right answer is (E) |  |
|
|
Comments |
casseverhart13
2019-10-01 03:22:05 | Good Examine and fascinating. Thanks. www.trustytreeservice.com |  | ernest21
2019-08-10 03:09:33 | Instead of doing the long division by hand, you could just say that gamma is less than 2. Solving the inequality you get that v > \\sqrt{3/4}c. E is the only answer that satisfies this. amino acid game |  | joshuaprice153
2019-08-08 07:30:34 | I\'m definitely going to bookmark your site, I just love your post, thanks for such a nice sharing.. Hope to get some info on your site in future. carpet steam cleaner |  | jeka
2007-02-17 08:08:36 | Energy spectrum of the hydrogen atom is given by the equation
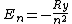 , ,
where 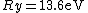 is the Rydberg constant. So the right answer is (E) is the Rydberg constant. So the right answer is (E)
FortranMan
2008-10-16 23:10:09 |
According to Griffiths, the allowed energies for a hydrogen atom are
![E_{n} = -\left[ \frac{m}{2 \hbar^2} \left(\frac{e^2}{4 \pi \epsilon_{0}}\right)^{2}\right] \frac{1}{n^2} = \frac{E_1}{n^2}](/cgi-bin/mimetex.cgi?E_{n} = -\left[ \frac{m}{2 \hbar^2} \left(\frac{e^2}{4 \pi \epsilon_{0}}\right)^{2}\right] \frac{1}{n^2} = \frac{E_1}{n^2} )
Where 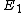 is the ground state of the hydrogen atom, is the ground state of the hydrogen atom,

The Rydberg constant is defined as
![R_{y} = \left[ \frac{m}{4 \pi c \hbar^3}\left(\frac{e^2}{4 \pi \epsilon_{0}}\right)^{2}\right] = 1.097 \times 10^{7} m^{-1}](/cgi-bin/mimetex.cgi?R_{y} = \left[ \frac{m}{4 \pi c \hbar^3}\left(\frac{e^2}{4 \pi \epsilon_{0}}\right)^{2}\right] = 1.097 \times 10^{7} m^{-1})
Thus the energy levels are given as
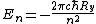
Not entirely necessary to solve the problem, but it's safer to keep your terms straight.
|
VKB
2014-03-25 21:44:48 |
Its a good approach to solve problems @ home,interesting.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
