|
GR0177 #83
|
|
|
|
|
Alternate Solutions |
wittensdog
2009-10-09 18:03:21 | In my opinion, you can completely forget about the information about z. You're given the form of the operator, and an expression for each of the possible choices. The up and down states could be any random vectors, disregard the information about what they represent. All you want to have happen is that when you act the matrix on one of the choices, you get the negative of it back out.
Quickly looking at the matrix, it's clear that it's just going to swap the positions of the two entries (if you want proof, act the matrix out on a vector of the form (x, y) and you'll get (y,x) ). The only choice that becomes the negative of itself when you swap the two components is C (technically speaking -hbar/2 will be the factor, since the actual spin operator has the factor of hbar/2 on it). It doesn't matter what the up and down symbols mean, the above is still true.
Perhaps more technically, you do need to know that the up and down states of the z operator form a basis, which can be used for all other spin orientations. But as long as you know that the spin eigenstates of one operator always can be used as a basis, then the choices you're looking at are really just vectors who happen to have their components in this one particular basis choice listed. |  | Herminso
2009-09-21 18:35:56 | Another alternative is to solve the eigenvalue problem for 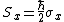 giving the eigenvalues giving the eigenvalues 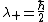 and and 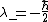 . .
Since we need the eigenstate of 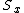 with eigenvalue with eigenvalue 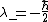 , we have , we have
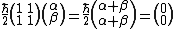  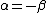 and by orthogonality and by orthogonality 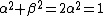  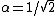 .Thus the eigenstate is just, .Thus the eigenstate is just,
![\begin{pmatrix} \alpha \\ \beta\end{pmatrix}=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}=\frac{1}{\sqrt{2}}\left[ \begin{pmatrix} 1 \\ 0\end{pmatrix}-\begin{pmatrix} 0 \\ -1\end{pmatrix} \right]=\frac{1}{\sqrt{2}}\left[ \langle\uparrow\rangle-\langle\downarrow\rangle \right]<br />](/cgi-bin/mimetex.cgi?\begin{pmatrix} \alpha \\ \beta\end{pmatrix}=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}=\frac{1}{\sqrt{2}}\left[ \begin{pmatrix} 1 \\ 0\end{pmatrix}-\begin{pmatrix} 0 \\ -1\end{pmatrix} \right]=\frac{1}{\sqrt{2}}\left[ \langle\uparrow\rangle-\langle\downarrow\rangle \right]<br />
)
|  | duckduck_85
2008-11-03 15:47:10 | It can be useful to remember the final state after a rotation in SU(2):
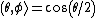(+\rangle z + e^{i\phi}sin(\theta/2)(-\rangle z)
For a rotation from z to x, plug in theta=pi/2 and phi=0 to get the answer. (C) |  |
|
|
Comments |
HYaorUan
2016-04-12 13:33:34 | This is just the equation 4.151 in Griffith\'s QM book. |  | apr2010
2010-04-09 15:21:23 | Regarding you have answered question 82 before: They ask about the symmetry of such a spin triplet and u might might notice that the only state who satisfy such a symmetry demanded in 82 is choice B). The symmetry in 83 is the same and forced with the given Pauli Matrix.
Genius these ETS people. |  | wittensdog
2009-10-09 18:03:21 | In my opinion, you can completely forget about the information about z. You're given the form of the operator, and an expression for each of the possible choices. The up and down states could be any random vectors, disregard the information about what they represent. All you want to have happen is that when you act the matrix on one of the choices, you get the negative of it back out.
Quickly looking at the matrix, it's clear that it's just going to swap the positions of the two entries (if you want proof, act the matrix out on a vector of the form (x, y) and you'll get (y,x) ). The only choice that becomes the negative of itself when you swap the two components is C (technically speaking -hbar/2 will be the factor, since the actual spin operator has the factor of hbar/2 on it). It doesn't matter what the up and down symbols mean, the above is still true.
Perhaps more technically, you do need to know that the up and down states of the z operator form a basis, which can be used for all other spin orientations. But as long as you know that the spin eigenstates of one operator always can be used as a basis, then the choices you're looking at are really just vectors who happen to have their components in this one particular basis choice listed. |  | Herminso
2009-09-21 18:35:56 | Another alternative is to solve the eigenvalue problem for 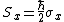 giving the eigenvalues giving the eigenvalues 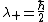 and and 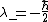 . .
Since we need the eigenstate of 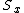 with eigenvalue with eigenvalue 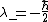 , we have , we have
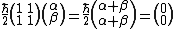  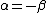 and by orthogonality and by orthogonality 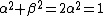  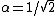 .Thus the eigenstate is just, .Thus the eigenstate is just,
![\begin{pmatrix} \alpha \\ \beta\end{pmatrix}=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}=\frac{1}{\sqrt{2}}\left[ \begin{pmatrix} 1 \\ 0\end{pmatrix}-\begin{pmatrix} 0 \\ -1\end{pmatrix} \right]=\frac{1}{\sqrt{2}}\left[ \langle\uparrow\rangle-\langle\downarrow\rangle \right]<br />](/cgi-bin/mimetex.cgi?\begin{pmatrix} \alpha \\ \beta\end{pmatrix}=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}=\frac{1}{\sqrt{2}}\left[ \begin{pmatrix} 1 \\ 0\end{pmatrix}-\begin{pmatrix} 0 \\ -1\end{pmatrix} \right]=\frac{1}{\sqrt{2}}\left[ \langle\uparrow\rangle-\langle\downarrow\rangle \right]<br />
)
|  | oSciL8
2009-03-30 20:18:07 | The last two tests worth of problems aren't loading for me! Under the problem banner, it says:rnrn"This problem is still being typed. "rnrnAnyone else having this problem? Any ideas how to resolve it?!?!
asafparis
2009-04-02 12:52:43 |
You can get the sample tests herernrnhttp://www.physics.ohio-state.edu/undergrad/ugs_gre.php
|
|  | cyp_phy
2009-03-29 10:48:41 | \sigma_1 = \sigma_x = \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}
\sigma_2 = \sigma_y = \begin{pmatrix} 0&-i\\ i&0 \end{pmatrix}
\sigma_3 = \sigma_z = \begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix}.
so it seems that answer ( c) |  | cyp_phy
2009-03-29 10:46:23 | i agree that the answer is (c) ... |  | duckduck_85
2008-11-03 15:47:10 | It can be useful to remember the final state after a rotation in SU(2):
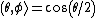(+\rangle z + e^{i\phi}sin(\theta/2)(-\rangle z)
For a rotation from z to x, plug in theta=pi/2 and phi=0 to get the answer. (C)
duckduck_85
2008-11-03 16:05:09 |
sorry, it's actually 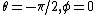
|
|  | tensordyne
2008-10-31 14:55:20 | It is not entirely clear from the answer given but it seems the author is saying the answer is (C), to wit I agree 100%. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
