|
GR0177 #80
|
|
|
|
|
Alternate Solutions |
nbwell
2007-10-29 00:27:39 | An alternative solution for this one could be to simply eliminate all the wrong ones, no need for all the fancy math above. Or perhaps combining an optical path length and lorentz factor would make a more mathy solution and avoid the confusing differential terms (I'll leave that to someone else).
The light is traveling through a non-vacuum medium, which almost immediately guarantees the overall speed is less than c regardless of the direction the tube is moving-so answer 'E' is out.
The speed of light in the tube is given by the refractive index formula c = v/n where v is the velocity in the medium and n is the medium's refractive index. If the tube were not moving at all, then the light's speed would appear to be (3/4)c and it would traverse a certain distance (s) in a certain amount of time. If the tube were moving at the speed of light, then the light's speed would appear to be c and it wouldn't appear to be travel any distance through the tube at all.
So for a tube traveling with a speed halfway between a non-moving tube and a light speed tube, a first guess solution would be to say the speed of light in the tube should be halfway between it's (3/4)c and c speed-say something around (7/8)c. Which suggests answers C or D.
Here's where it gets a little hand-wavey. Knowing that the lab frame distance traveled is s/gamma or that the lab frame time is t/gamma (where gamma is a Lorentz factor greater than one) suggests that the relative space or time in the tube's reference frame is compressed->resulting in the the light traveling faster in the lab frame than the (7/8)c calculated above. The only answer less than C but greater than (7/8)c is answer D. |  |
|
|
Comments |
Crand0r
2010-11-11 16:58:11 | As has been stated (without the Typo flag), the third equation in yosun's solution (the equation for 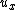 ) should have a factor of ) should have a factor of 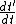 on the last expression. on the last expression. |  | iamSMRT
2009-11-06 23:13:29 | This was how I did it quickly:
The beam of light should be travelling through the water at 3/4*c, while the tube itself is travelling at 1/2*c. Use the addition of relativistic velocities equation and get:
v =  = =  = =  . Answer (D) . Answer (D) |  | kroner
2009-10-05 12:35:46 | The formula for adding relativistic velocities is probably a good one to know.
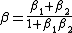 , or , or 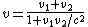
uhurulol
2014-10-21 19:01:07 |
Thank you for this answer. The GRE is all about the quickest method possible, and while Yosun's is well done, I would absolutely hate to go through all that in 1.7 minutes. I would have completely forgotten about addition of relativistic velocities if it weren't for this comment!
|
|  | nbwell
2007-10-29 00:27:39 | An alternative solution for this one could be to simply eliminate all the wrong ones, no need for all the fancy math above. Or perhaps combining an optical path length and lorentz factor would make a more mathy solution and avoid the confusing differential terms (I'll leave that to someone else).
The light is traveling through a non-vacuum medium, which almost immediately guarantees the overall speed is less than c regardless of the direction the tube is moving-so answer 'E' is out.
The speed of light in the tube is given by the refractive index formula c = v/n where v is the velocity in the medium and n is the medium's refractive index. If the tube were not moving at all, then the light's speed would appear to be (3/4)c and it would traverse a certain distance (s) in a certain amount of time. If the tube were moving at the speed of light, then the light's speed would appear to be c and it wouldn't appear to be travel any distance through the tube at all.
So for a tube traveling with a speed halfway between a non-moving tube and a light speed tube, a first guess solution would be to say the speed of light in the tube should be halfway between it's (3/4)c and c speed-say something around (7/8)c. Which suggests answers C or D.
Here's where it gets a little hand-wavey. Knowing that the lab frame distance traveled is s/gamma or that the lab frame time is t/gamma (where gamma is a Lorentz factor greater than one) suggests that the relative space or time in the tube's reference frame is compressed->resulting in the the light traveling faster in the lab frame than the (7/8)c calculated above. The only answer less than C but greater than (7/8)c is answer D.
djh101
2014-09-07 23:41:53 |
Great answer.
|
UNKNOWNUMBER
2018-10-20 20:18:49 |
It\'s v = c/n
|
|  | madfish
2007-10-09 17:49:37 | I have a qualm with this problem...I thought the speed of light c does not depend on the velocity of the inertial frame (Einstein's 3rd postulate of relativity). That being said, the fact that the tube of water is moving should not effect the "c" value, so the only thing that should is the medium change....Where has my reasoning gone wrong here?
Shtego
2007-10-09 21:38:20 |
Agree! The only thing I can figure is that you're right. However, perhaps the resulting length contraction of the moving water tube alters the index of refraction of the moving tube of water, which in turns results in a different speed of light measurment in the lab frame than of the proper frame. Any other ideas?
|
kyros
2007-10-28 13:20:44 |
Einstein's 3rd postulate says that the speed of light in a vacuum is the same in all inertial frames. The propogation of electromagnetic waves in a media is DRAMATICALLY different physically. It is no surprise given the complex interactions required by the electric fields in matter for light to travel through it, that a velocity transform would shift the velocity of light.
|
Poop Loops
2008-11-01 21:05:19 |
The speed of light in the medium is c/n not because the speed slows down, but because light constantly bumps into atoms and has to get re-emitted.
Now, you are saying that it shouldn't matter how fast the material is moving, the index of refraction should stay the same, correct? Well, when the material is moving at 1/2*c, it undergoes length contraction. In the lab frame it is "squeezed", which also gives it a higher density, which can definitely change the index of refraction.
|
Albert
2009-10-29 10:26:19 |
Hey, I would have thought that the length contraction is mostly virtual. And inside the thing which is moving at high speed, the length would remain the same. Hence, it is only an outsider who, when sees the moving thing, will see it become smaller.
After the light has entered the tube, it should treat the tube as if it were stationary. Then, why does it not? If that were to be, shouldn't (2/3)*c be the right answer? But it's not and I know I am wrong, but why, is what I am unsure of.
|
sina2
2013-09-15 02:51:23 |
I agree with "Poop Loops". I did wrong on choosing C as invariant speed too. But passing through a different medium defines a new condition. Density could be so cheating. The interaction with higher atoms leads to less speed.
|
|  | erc
2005-11-10 16:52:08 | Typo alert: missing 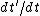 at end of expression for at end of expression for 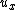 I think. I think.
Blake7
2007-09-21 23:19:09 |
Yup, me too; dt'/dt looks to be missing for the ux expression
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
