|
GR0177 #70
|
|
|
|
|
Alternate Solutions |
carle257
2010-04-01 23:04:36 | Recall also that as the wavelength becomes small compared to the slit, the spread of the fringes will become smaller. If you remember that the separation is linear in  then you can deduce answer (B) which is half of the original separation. Just another way of looking at it without remembering the exact diffraction equations. |  |
|
|
Comments |
Ddrew
2012-08-08 04:27:12 | Recall the formula for the distance between fringles 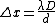 , where D is a distance between a screen and a source of light; d stands for a distance between slits.
From here, once easly could rewrite for frequency 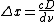 . |  | D-Rock
2010-09-18 17:58:36 | You know from a vague memory of diffraction formulas that this will be linear (I mean, 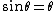 here), and if your wavelength's tiny enough, they won't even see the slits, so limiting case gives that the angles will go to zero, hence it must B. | | carle257
2010-04-01 23:04:36 | Recall also that as the wavelength becomes small compared to the slit, the spread of the fringes will become smaller. If you remember that the separation is linear in then you can deduce answer (B) which is half of the original separation. Just another way of looking at it without remembering the exact diffraction equations. | | tau1777
2008-11-03 19:35:02 | i can't really tell if this is the same solution as what's been posted. so here goes: constructive interference for double slit is given by 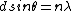 . then i made a small angle approximation (really for fun, just assuming that it could be done, and since we have no info about angles) so we get 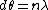 . then remembering that  where R is the distance from the slits to the screen, and 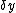 is a height on the screen from y=0 where maximum interference peak is. then solving for solving for theta, and setting the equations equal to one another we get 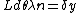 . then we know that if frequency gets doubled the wavelength should be halved and then the distances  on the screen will also be halved.
chemicalsoul
2009-10-30 00:19:40 |
I did this way too.
|
| | phys2718
2008-09-28 10:28:17 | This is not a single slit interference problem, it is a double slit problem - and d is the distance between the very narrow slits, not the width of a slit. The interference maxima equation is however correct ( but for the DOUBLE slit problem). | |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
