|
GR0177 #61
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Boundary Conditions }Boundary Conditions
For a conductor, the electric field boundary condition at the interface are 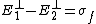 ( (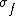 is the free charge density) and is the free charge density) and 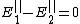 . .
The plane wave traveling in the x-direction is polarized (say) in the +z-direction. Thus, 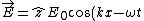) . .
There is no component perpendicular to the conductor at the boundary, and thus the first boundary condition implies that the free charge density is 0.
The second boundary condition requires that 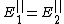 . The parallel component of E is polarized in the z-direction, and thus the requirement is . The parallel component of E is polarized in the z-direction, and thus the requirement is  , i.e., the incident plus the reflected is equal to the transmitted wave. However, for a perfect conductor, the transmitted wave is 0. Thus, one has , i.e., the incident plus the reflected is equal to the transmitted wave. However, for a perfect conductor, the transmitted wave is 0. Thus, one has 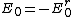 . This implies that the electric field to the left of the conductor cancels. . This implies that the electric field to the left of the conductor cancels.
Recall the Poynting vector,  , which conveniently points in the direction of the electromagnetic wave propagation. Since the electric field (by the convention used above) is polarized in the z-direction, the magnetic field of the incident wave points in the -y direction. However, since the electric field of the reflecting wave points in the -z-direction, its magnetic field also points in the -y direction. The magnetic field magnitude is thus , which conveniently points in the direction of the electromagnetic wave propagation. Since the electric field (by the convention used above) is polarized in the z-direction, the magnetic field of the incident wave points in the -y direction. However, since the electric field of the reflecting wave points in the -z-direction, its magnetic field also points in the -y direction. The magnetic field magnitude is thus 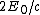 . Hence, one has choice (C). . Hence, one has choice (C).
|
|
|
Alternate Solutions |
yummyhat
2017-10-26 19:41:40 | almost every comment is wrong! we are asked for the behavior on the LEFT side of the boundary, i.e. reflection. the official solution is correct, but to explain it qualitatively: conductors cannot support electric fields, so the E field cannot penetrate the plane (and therefore no energy is carried through it). standing waves (no time dependence) do not transfer energy, so this is what is produced.\r\n\r\nby looking at the boundary conditions, we see that E at the surface of the conductor must be zero (because the E field inside the conductor is zero). in other words, the boundary condition fixes a node for E at the surface of the conductor. the B wave is phase shifted by ninety degrees with respect to the E wave, hence B must be at an antinode at the surface of the conductor, and it therefore interferes with itself constructively. \r\n\r\none could predict this by noticing that a phase difference of ninety degrees will zero the poynting vector, which is a description of energy transfer. \r\n\r\nalso, it seems important that if you move away from the surface of the conductor, you leave the node-antinode plane and things are a bit more complicated until the next node-antinode plane. this is why the question specifies that we are discussing the location IMMEDIATELY to the left of the plane. maybe that explains why everyone who took the exam missed it.. xD |  | ramparts
2009-10-08 12:17:53 | Even more simply put - a conductor sets the E field to 0, and multiplies the B field by 2. That's C.
That's how I solved it, but as mentioned in the comments, knowing that E is set to 0 and B isn't (and B isn't 0 to begin with, as an EM wave can't be all E) is all you need to pick C. |  | SonOfOle
2006-10-31 21:22:48 | More simply put, from a conceptual level.
1) E fields don't propagate through conductors. So E=0.
2) The E field incident on the conductor moves the charges back and forth of the conductor, which in turn set up an oscillating B-field to the right of the conductor. So B is oscillating.
3) Answer (C) is the only one that satisfies both these conditions. |  |
|
|
Comments |
yummyhat
2017-10-26 19:41:40 | almost every comment is wrong! we are asked for the behavior on the LEFT side of the boundary, i.e. reflection. the official solution is correct, but to explain it qualitatively: conductors cannot support electric fields, so the E field cannot penetrate the plane (and therefore no energy is carried through it). standing waves (no time dependence) do not transfer energy, so this is what is produced.\r\n\r\nby looking at the boundary conditions, we see that E at the surface of the conductor must be zero (because the E field inside the conductor is zero). in other words, the boundary condition fixes a node for E at the surface of the conductor. the B wave is phase shifted by ninety degrees with respect to the E wave, hence B must be at an antinode at the surface of the conductor, and it therefore interferes with itself constructively. \r\n\r\none could predict this by noticing that a phase difference of ninety degrees will zero the poynting vector, which is a description of energy transfer. \r\n\r\nalso, it seems important that if you move away from the surface of the conductor, you leave the node-antinode plane and things are a bit more complicated until the next node-antinode plane. this is why the question specifies that we are discussing the location IMMEDIATELY to the left of the plane. maybe that explains why everyone who took the exam missed it.. xD |  | calvin_physics
2014-04-03 19:51:48 | I remember from previous physics GRE problem, it asked what's the direction of reflected E field.
So certainly SonOfOle's explanation is inadequate. E fields don't propagate through conductors doesn't necessarily mean E = 0 in all cases.
For this problem, it asks "the total E field" which is 0 because it cancels out the incident wave.
However, now I have a question, how do you know if they are canceled out? What if my incident wave isn't continuously hitting on the plane? Eventually the reflected E field will take over and it's not 0 anymore.
dwm
2015-10-18 12:42:18 |
The electrons in the metal are totally free, as the conductor is perfect. Therefore, the barrier can be thought of as \"loose.\" When a wave on a string hits a loose boundary, the reflected component is perfectly out of phase with the incident component. Similarly, the incident and reflected E fields are out of phase and cancel each other out. In some sense, you\'re both right. There are two equal and opposite E fields at the conductor surface, one incident and the other reradiated by the moving charges; they sum to zero.
|
|  | kiselev
2011-04-01 12:29:07 | First of all, I'd like to thank everyone for their support given to people who are going to take this test. Thanks to Yosun, for this excellent website and to Taylor in physicsgrad.comrnI would like to point out some important things in this problem that came out from Prof Lewis lecture, Theoretical and experimental way! :D I love physics (that is also an excellent material fro preparing for PGRE) http://www.youtube.com/watch?v=rp1orH7OC1c&feature=player_embedded.rnrnI think we all have clear that 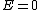 (boundary conditions of E), but what it is not obvious is that there is going to be standing waves in the left . Moreover, B is gonna be also a standing wave but out of phase 90 degrees in space and time! the 2 factor comes from standing waves too.rnrnCan you think what happens in the right side?rnrnI have learned a lot from this problem and Prof. Walter Lewin. rnMaybe this post would be helpful to somebody else.rnCheers!rnrn (boundary conditions of E), but what it is not obvious is that there is going to be standing waves in the left . Moreover, B is gonna be also a standing wave but out of phase 90 degrees in space and time! the 2 factor comes from standing waves too.rnrnCan you think what happens in the right side?rnrnI have learned a lot from this problem and Prof. Walter Lewin. rnMaybe this post would be helpful to somebody else.rnCheers!rnrn
NoPhysicist
2017-03-16 09:44:16 |
what the heck man are you typing here
|
|  | Grandpsykick
2010-03-11 15:20:18 | Even more simply put:
1) E fields don't propagate through conductors (if they are normal to the surface).
2) The energy in the field MUST be transmitted through the surface.
3) E is zero (0), thus B cannot be zero (0); thus, the only answer is C.
NOTE: you didn't need any math, or "wave dynamics", or anything but simple knowledge of EM and conservation of energy. |  | ramparts
2009-10-08 12:17:53 | Even more simply put - a conductor sets the E field to 0, and multiplies the B field by 2. That's C.
That's how I solved it, but as mentioned in the comments, knowing that E is set to 0 and B isn't (and B isn't 0 to begin with, as an EM wave can't be all E) is all you need to pick C. |  | Gaffer
2007-10-23 13:54:30 | Do be careful about the question. It asks for the fields to the left of the conductor - that is the side of incidence, not transmittance.
To be accurate, you need the original approach.
Gaffer
2007-10-23 13:55:44 |
TO clairify, I was agreeing with the author, not SonOfOle. What he said was correct, but his comment indicates he was looking at the improper side.
|
Jeremy
2007-10-25 11:58:59 |
I think SonOfOle's conceptual approach works if you replace his (1) with:
(1) Conductors only allow perpendicular electric fields at their boundaries, so 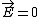 on both sides. on both sides.
|
|  | SonOfOle
2006-10-31 21:22:48 | More simply put, from a conceptual level.
1) E fields don't propagate through conductors. So E=0.
2) The E field incident on the conductor moves the charges back and forth of the conductor, which in turn set up an oscillating B-field to the right of the conductor. So B is oscillating.
3) Answer (C) is the only one that satisfies both these conditions.
anmuhich
2009-03-15 12:54:45 |
Right! And you don't even need to know the B field is oscillating, just that there is a B field and no E field! The electrons in the conductor arrange themselves in such a way with the E field as to cancel its affect. However, you know a B field must be induced anytime you have moving charge.
|
anmuhich
2009-03-15 13:02:06 |
Sorry it's the oscillating E field that causes the induced B field.
|
walczyk
2011-04-07 18:13:03 |
awesome description
|
NoPhysicist
2017-03-16 09:41:16 |
Why would you consider field to the right of the plane?
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
