|
GR0177 #5
|
|
|
Problem
|
|
|
This problem is still being typed. |
Thermodynamics }Degree of Freedom }Degree of Freedom
Acording to the Equipartition Theorem, there is a $kt/2$ contribution to the energy from each degree of quadratic freedom in the Hamiltonian. In equation form, the average total energy is 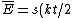) , where s is the degrees of freedom. , where s is the degrees of freedom.
For a n-dimensional 1-particle system, the Hamiltonian is 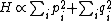 , where , where  ( ( ) refer, respectively, to the ) refer, respectively, to the 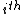 component of momentum (position). component of momentum (position).
Thus, for a 3-dimensional 1-particle system, one has 6 quadratic terms in the Hamiltonian, as in  . .
Plugging in s=6, one finds that the average energy is 3kT.
(This revised solution is due to the GREPhysics.NET user kolndom.)
|
|
|
Alternate Solutions |
kolndom
2005-11-09 20:38:28 | hi
In my opinion, we need only to consider the equipartition theorem, which reads for a system with single molucule energy E=Ap^2+Bq^2 each squared momentum or displacement term has same average kT/2. Since there are three translational degrees of freedom and 3 vibrational degrees of freedom and 3 rotational degrees of freedom, the total energy is (3+3)*kT/2=3kT.
daschaich
2005-11-09 21:24:22 |
There was a lot of discussion of this problem on the physicsgre yahoo group mailing list a few weeks back. Gbadebo Olaosebikan settled it with the following post. You can check out the earlier posts by poking around at
http://groups.yahoo.com/group/physicsgre/message/2378 />
// --------------------------
I think reibaretti's answer is the "right one" because
it uses the exact statement of the equipartition
theorem without any assumptions of the nature of the
oscillator.
The "n" in nKT/2 , we must remember strictly is
defined as the number of "squared" or quadratic terms
in the enrgy of a system. That this turns out to be
the number of degrees of freedom is only a corollary.
the energy of a three d oscillator which must be
assumed a particle UNLESS otherwise stated is
E = T + U
T = ((p_x)^2 + (p_y)^2 + (p_z)^2)/2m
U= mw^2(x^2 +y^2 +z^2)/2
There are definitely 6 "squared terms" in the energy E and so n=6 and the average energy becomes 6(kT/2)= 3kT.
Cheers
Debo
// --------------------------
|
daschaich
2005-11-09 21:25:56 |
Which is exactly what kolndom wrote... sorry, didn't see your comment.
|
NaijaProfessor
2005-12-05 22:15:51 |
A 3 dimensional harmonic oscillator has six degrees of freedom, 3 for KE and 3 for PE. Thus 6(1/2KT) = 3KT.
cheers.
|
yosun
2005-12-06 19:15:48 |
kolndom, daschaich, NaijaProfessor --- thank you for flagging this problem; I have revised the solution above.
|
|  |
|
|
Comments |
Ithillhoss
2015-10-10 03:16:01 | According to the equipartition theorem, the average energy of the system equals to 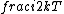 , where , where 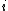 is degree of freedom, the number of coordinates need to determined the configuration of system uniquely. So there is 3 translational 2 rotational (diatomic molecule) + 1 vibrational =6 degrees of freedom. So the correct answer is is degree of freedom, the number of coordinates need to determined the configuration of system uniquely. So there is 3 translational 2 rotational (diatomic molecule) + 1 vibrational =6 degrees of freedom. So the correct answer is 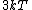 . . |  | buaasyh
2015-08-24 15:00:29 | Checking Wikipedia for equipartition theorem, I think it is more appropriate to say the six degrees of freedom include three for kinetic energy and three for potential energy (instead of three for translation and three for rotation) as in the example of heat capacity of solids there. The original answer in terms of Hamiltonian (kinetic energy plus potential energy by definition) follows the same essence. |  | calvin_physics
2014-04-03 16:07:01 | How come diatomic atom only has 1 vibrational mode while harmonic oscillator has 3? |  | nvp10
2014-04-01 16:28:14 | If you have looked at the degrees of freedom of molecules you will be familiar with the fact that each vibrational mode corresponds to 2 degrees of freedom ( eg at high T a diatomic molecule has 3 translational + 2 rotational + 2x1 vibrational = 7 DOF, note there is only one mode of vibration).
A 3D SHO has 0 translational (can't move) + 0 rotational (spherical symmetry) + 2x3 vibrational (can vibrate in 3 directions) = 6 DOF. |  | thesandrus86
2011-04-24 14:32:02 | considero que es así:
por el teorema de equipartición de la energía tenemos que ésta es equivalente a ikT/2 para cada grado de libertad, se nos dice que es tridemensional, por lo tanto la respuesta es3kT/2
thesandrus86
2011-04-24 14:35:02 |
uhmmm claro! sumando sus grados de libertad la primera tendra tres, la segunda y tercera dos. por lo tanto tendremos en total 6kT/2...es decir: 3kT.
|
|  | T
2005-11-10 18:56:23 | |  | kolndom
2005-11-09 20:38:28 | hi
In my opinion, we need only to consider the equipartition theorem, which reads for a system with single molucule energy E=Ap^2+Bq^2 each squared momentum or displacement term has same average kT/2. Since there are three translational degrees of freedom and 3 vibrational degrees of freedom and 3 rotational degrees of freedom, the total energy is (3+3)*kT/2=3kT.
daschaich
2005-11-09 21:24:22 |
There was a lot of discussion of this problem on the physicsgre yahoo group mailing list a few weeks back. Gbadebo Olaosebikan settled it with the following post. You can check out the earlier posts by poking around at
http://groups.yahoo.com/group/physicsgre/message/2378 />
// --------------------------
I think reibaretti's answer is the "right one" because
it uses the exact statement of the equipartition
theorem without any assumptions of the nature of the
oscillator.
The "n" in nKT/2 , we must remember strictly is
defined as the number of "squared" or quadratic terms
in the enrgy of a system. That this turns out to be
the number of degrees of freedom is only a corollary.
the energy of a three d oscillator which must be
assumed a particle UNLESS otherwise stated is
E = T + U
T = ((p_x)^2 + (p_y)^2 + (p_z)^2)/2m
U= mw^2(x^2 +y^2 +z^2)/2
There are definitely 6 "squared terms" in the energy E and so n=6 and the average energy becomes 6(kT/2)= 3kT.
Cheers
Debo
// --------------------------
|
daschaich
2005-11-09 21:25:56 |
Which is exactly what kolndom wrote... sorry, didn't see your comment.
|
NaijaProfessor
2005-12-05 22:15:51 |
A 3 dimensional harmonic oscillator has six degrees of freedom, 3 for KE and 3 for PE. Thus 6(1/2KT) = 3KT.
cheers.
|
yosun
2005-12-06 19:15:48 |
kolndom, daschaich, NaijaProfessor --- thank you for flagging this problem; I have revised the solution above.
|
physicsman
2010-01-18 22:27:50 |
It should be noted in the solution that the potential degrees of freedom come form being an harmonic oscillator. If this was a free particle only the translation terms would show up and the energy would be halved
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
